题目内容
已知正数a,b满足a2+b2=2,则下列结论错误的是
- A.ab≤1
- B.a+b≤2
- C.
 ≤2
≤2 - D.
 ≤2
≤2
D
分析:先利用均值定理a2+b2≥2ab,证明ab≤1正确,再利用此结论将a+b, 平方后证明B、C正确,最后通过举反例的办法证明D错误
平方后证明B、C正确,最后通过举反例的办法证明D错误
解答:∵a2+b2=2≥2|ab|,∴ab≤1正确;
∵(a+b)2=a2+b2+2ab=2+2ab≤4,∴a+b≤2正确;
∵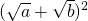 =a+b+2
=a+b+2 ≤2+2=4,∴
≤2+2=4,∴ ≤2正确;
≤2正确;
若a= ,b=
,b= ,则
,则 >2,故
>2,故 ≤2错误
≤2错误
故选D
点评:本题考查了不等式的基本性质,均值定理及其运用,推理证明的能力
分析:先利用均值定理a2+b2≥2ab,证明ab≤1正确,再利用此结论将a+b,
 平方后证明B、C正确,最后通过举反例的办法证明D错误
平方后证明B、C正确,最后通过举反例的办法证明D错误解答:∵a2+b2=2≥2|ab|,∴ab≤1正确;
∵(a+b)2=a2+b2+2ab=2+2ab≤4,∴a+b≤2正确;
∵
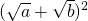 =a+b+2
=a+b+2 ≤2+2=4,∴
≤2+2=4,∴ ≤2正确;
≤2正确;若a=
 ,b=
,b= ,则
,则 >2,故
>2,故 ≤2错误
≤2错误故选D
点评:本题考查了不等式的基本性质,均值定理及其运用,推理证明的能力

练习册系列答案
相关题目
 的最大值;
的最大值;  的最小值。
的最小值。