题目内容
是否存在△ABC,使得顶点A(4,4),∠B的平分线所在直线方程l1:x-y-4=0,∠C的平分线所在直线方程l2:x+3y-8=0?如果存在,请求出此三角形三边所在直线的方程;如果不存在,请说明理由.
思路分析：只要计算A(4,4)关于l1、l2的对称点M、N,直线MN就是所求三角形的BC边所在直线方程.同理可得其余两边所在直线方程.故存在这样的确定的△ABC.
解：设A(4,4)关于l1的对称点M(x1,y1),
则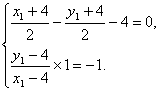
∴M(8,0).
同理可得A(4,4)关于l2的对称点N的坐标为(
),
∴lBC的方程为x-7y-8=0.
又∵
可得B(
,-
).
∴lAB的方程为7x-y-24=0.
同理可得lAC的方程为x+y-8=0.
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
如图，在底面是菱形的四棱锥P-ABCD中，∠ABC=60°，PA=AC=a，PB=PD=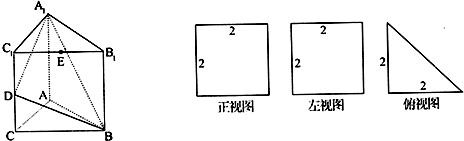
直三棱柱A1B1C1-ABC的三视图如图所示，D、E分别为棱CC1和B1C1的中点．
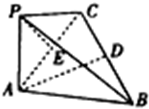如图，在三棱锥P-ABC中，PA⊥平面ABC，AB=AC，∠BAC为直角，D，E分别为BC，AC的中点，AB=2PA=4．
如图，在正四棱锥S-ABCD中，AB=
的图象上有A、B两动点，满足AB∥x轴，点M(1,m)(m为常数，m>3)是三角形ABC的边BC的中点，设A点横坐标t，△ABC的面积为f (t).