题目内容
13.已知f(x)=xlnx,设其切线为L(1)求f(x)在(1,0)处切线方程L;
(2)证明:除切点外,f(x)的图象一直在L上方.
分析 (1)求出函数的导数,求得切线的斜率,由点斜式方程即可得到切线方程;
(2)令g(x)=f(x)-x+1=xlnx-x+1(x>0),求出g(x)的导数,求得单调区间和极值、最值,即可得证.
解答 (1)解:f(x)=xlnx的导数为f′(x)=lnx+1,
即有f(x)在(1,0)处切线斜率为k=1,
则f(x)在(1,0)处切线方程l为y=x-1;
(2)证明:令g(x)=f(x)-x+1=xlnx-x+1(x>0),
g′(x)=lnx+1-1=lnx,
当x>1时,g′(x)>0,g(x)递增;
当0<x<1时,g′(x)<0,g(x)递减.
即有x=1处g(x)取得极小值,也为最小值,且为0.
则有g(x)≥0,
即有xlnx≥x-1.
故除切点外,f(x)的图象一直在l上方.
点评 本题考查导数的运用:求切线方程和单调区间、极值及最值,主要考查导数的几何意义,同时考查转化思想的运用,属于中档题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
18.阅读下列算法:
(1)输入x.
(2)判断x>2是否成立,若是,y=x; 否则,y=-2x+6.
(3)输出y.
当输入的x∈[0,7]时,输出的y的取值范围是( )
(1)输入x.
(2)判断x>2是否成立,若是,y=x; 否则,y=-2x+6.
(3)输出y.
当输入的x∈[0,7]时,输出的y的取值范围是( )
| A. | [2,7] | B. | [2,6] | C. | [6,7] | D. | [0,7] |
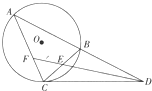 如图所示,已知A、B、C三点都在⊙O上,CD是⊙O的切线,直线AB与CD交于点D.
如图所示,已知A、B、C三点都在⊙O上,CD是⊙O的切线,直线AB与CD交于点D.