题目内容
已知函数 是奇函数,且
是奇函数,且 .
.
(Ⅰ)求实数m和n的值;
(Ⅱ)判断函数f(x)在(-∞,-1]上的单调性,并加以证明.
解:(Ⅰ)∵函数 是奇函数
是奇函数
∴f(-x)=-f(x)
∴
∴n=0
∵ .
.
∴
∴m=2
(II)函数f(x)在(-∞,-1]上是增函数
证明:任取
 =
= ∵x1<x2<-1,∴x1-x2<0,x1x2-1>0
∵x1<x2<-1,∴x1-x2<0,x1x2-1>0
∴f(x1)-f(x2)<0
∴f(x1)<f(x2)
∴函数f(x)在(-∞,-1]上是增函数
分析:(I)由函数是奇函数的,∴f(-x)=-f(x)恒成立,再用待定系数法求得m,n或找到m,n的关系,然全结合 求解.
求解.
(II)用单调性定义证明,先在给定区间上任取两个变量,且界其大小,再作差变形看符号.当自变量变化与函数值变化一致时,为增函数,当自变量变化与函数值变化相反时,为减函数.
点评:本题主要考查函数的奇偶性解题,一般情况下,已知奇偶性时,用待定系数法求解问题;同时还考查了用单调性定义证明函数的单调性,要注意变形要到位.
 是奇函数
是奇函数∴f(-x)=-f(x)
∴

∴n=0
∵
 .
.∴

∴m=2
(II)函数f(x)在(-∞,-1]上是增函数
证明:任取

 =
= ∵x1<x2<-1,∴x1-x2<0,x1x2-1>0
∵x1<x2<-1,∴x1-x2<0,x1x2-1>0∴f(x1)-f(x2)<0
∴f(x1)<f(x2)
∴函数f(x)在(-∞,-1]上是增函数
分析:(I)由函数是奇函数的,∴f(-x)=-f(x)恒成立,再用待定系数法求得m,n或找到m,n的关系,然全结合
 求解.
求解.(II)用单调性定义证明,先在给定区间上任取两个变量,且界其大小,再作差变形看符号.当自变量变化与函数值变化一致时,为增函数,当自变量变化与函数值变化相反时,为减函数.
点评:本题主要考查函数的奇偶性解题,一般情况下,已知奇偶性时,用待定系数法求解问题;同时还考查了用单调性定义证明函数的单调性,要注意变形要到位.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目

 是奇函数,且
是奇函数,且
 ,
, 的值;
的值; 在区间
在区间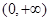 上是减函数.
上是减函数.  是奇函数,且在区间
是奇函数,且在区间 上单调递减,则
上单调递减,则 上是( )
上是( )  B. 单调递减函数,且有最大值
B. 单调递减函数,且有最大值 D.
单调递增函数,且有最大值
D.
单调递增函数,且有最大值 是奇函数,且
是奇函数,且 .
. 上的单调性,并加以证明.
上的单调性,并加以证明.  是奇函数,且图像在点
是奇函数,且图像在点
 为自然对数的底数)处的切线斜率为3.
为自然对数的底数)处的切线斜率为3. 、
、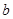 的值;
的值; ,且
,且 对任意
对任意 恒成立,求
恒成立,求 的最大值;
的最大值; 时,证明:
时,证明:
 是奇函数,且满足
是奇函数,且满足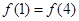
 、
、 的值;
的值;
 在区间
在区间 单调递减,在区间
单调递减,在区间 单调递增;
单调递增; 同时满足以下两个条件:1不等式
同时满足以下两个条件:1不等式 对
对 恒成立;
2方程
恒成立;
2方程 在
在 上有解.若存在,试求出实数
上有解.若存在,试求出实数