题目内容
已知函数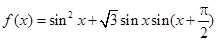 .
.
(1)求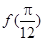 的值;
的值;
(2)当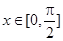 时,求函数
时,求函数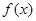 的最大值和最小值.
的最大值和最小值.
(1)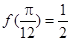 ;(2)最小值
;(2)最小值 ,最大值
,最大值 .
.
解析试题分析:本题主要考查诱导公式、倍角公式、降幂公式、两角和与差的正弦公式、三角函数最值等基础知识,考查学生的分析问题解决问题的能力、运用数学公式计算的能力,考查学生的数形结合思想.第一问,先利用诱导公式、倍角公式、降幂公式、两角和与差的正弦公式化简表达式,使之化简为 的形式,再将
的形式,再将 代入求三角函数值;第二问,将已知x的范围代入第一问化简的表达式中,求出角
代入求三角函数值;第二问,将已知x的范围代入第一问化简的表达式中,求出角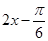 的范围,再数形结合得到最大值和最小值.
的范围,再数形结合得到最大值和最小值.
(1)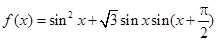
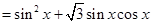
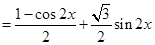
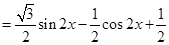
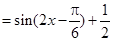 .
.
所以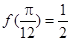 . 7分
. 7分
(2)当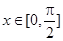 时,
时,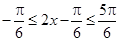 .
.
所以,当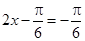 时,即
时,即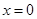 时,函数
时,函数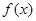 取得最小值
取得最小值 ;
;
当 时,即
时,即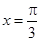 时,函数
时,函数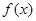 取得最大值
取得最大值 . 13分
. 13分
考点:诱导公式、倍角公式、降幂公式、两角和与差的正弦公式、三角函数最值.

练习册系列答案
相关题目
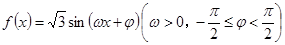 的图像关于直线
的图像关于直线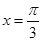 对称,且图像上相邻两个最高点的距离为
对称,且图像上相邻两个最高点的距离为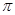 .
.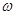 和
和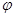 的值;
的值;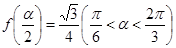 ,求
,求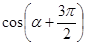 的值.
的值. 在
在 内只取到一个最大值和一个最小值,且当
内只取到一个最大值和一个最小值,且当 时,
时, ;当
;当 时,
时, .(1)求此函数的解析式;(2)求此函数的单调递增区间.
.(1)求此函数的解析式;(2)求此函数的单调递增区间.
 和角
和角 的终边分别与单位圆交于
的终边分别与单位圆交于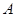 ,
, 两点,(其中
两点,(其中
 ,点
,点 ,求
,求 的值;
的值; , 求
, 求 的值.
的值.
 x﹣
x﹣ ),x∈R.
),x∈R. ,f(3
,f(3 )=
)=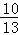 ,f(3β+
,f(3β+ )=
)= .求sin(α+β)的值.
.求sin(α+β)的值.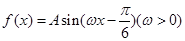 相邻两个对称轴之间的距离是
相邻两个对称轴之间的距离是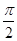 ,且满足,
,且满足,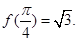
 的单调递减区间;
的单调递减区间; ,求△ABC的面积。
,求△ABC的面积。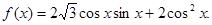
 的值;
的值; 时,求函数
时,求函数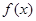 的值域.
的值域.
 的值.
的值.