题目内容
已知A,B,C三点不共线,对平面外任一点,满足条件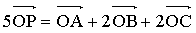 ,
,
试判断:点P与A,B,C是否一定共面?
思路分析:如果向量a、b不共线,则向量p与a、b共面的充分必要条件是存在实数对x,y,使p=xa+yb.则p、a、b三个向量上面的所有点在同一平面上.
解:![]() ,
,
则(![]() )=2(
)=2(![]() )+2(
)+2(![]() ),故
),故![]() ,即
,即![]() .所以,点P与A,B,C共面.
.所以,点P与A,B,C共面.
方法归纳 ①本题借助考察点的共面问题间接的考查了空间向量共面的问题,可以得到:在判定点的共面问题时转化为过这些点的向量共线问题来加以解决是一个行之有效的途径.
②如果存在O和不共线的三点A,B,C,并且![]() (x+y+z=1)则点P与点A,B,C共面,这个结论在解答填空、选择题时可以直接运用.
(x+y+z=1)则点P与点A,B,C共面,这个结论在解答填空、选择题时可以直接运用.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
已知A、B、C三点不共线,且点O满足
+
+
=0,则下列结论正确的是( )
| OA |
| OB |
| OC |
A、
| ||||||||||
B、
| ||||||||||
C、
| ||||||||||
D、
|
已知A、B、C三点不共线,O是平面ABC外的任一点,下列条件中能确定点M与点A、B、C一定共面的是( )
A、
| ||||||||||||||
B、
| ||||||||||||||
C、
| ||||||||||||||
D、
|