题目内容
如果lg m+lg n=0，那么m+n的最小值是 ________．
2
分析：先根据条件求出m、n满足的关系，再根据均值不等式求出m+n的最小值，注意等号成立的条件即可．
解答：∵lg m+lg n=0
∴lgmn=0=lg1即mn=1
∵m＞0，n＞0
∴m+n≥2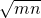
=2
故答案为2
点评：本题主要考查了对数函数的单调性，以及均值不等式的应用，属于基础题．
分析：先根据条件求出m、n满足的关系，再根据均值不等式求出m+n的最小值，注意等号成立的条件即可．
解答：∵lg m+lg n=0
∴lgmn=0=lg1即mn=1
∵m＞0，n＞0
∴m+n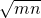≥2
=2故答案为2
点评：本题主要考查了对数函数的单调性，以及均值不等式的应用，属于基础题．
练习册系列答案
相关题目