题目内容
设 是两个不共线的非零向量,则“向量
是两个不共线的非零向量,则“向量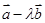 与
与 共线”是“
共线”是“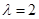 ”
”
的( )
| A.充分非必要条件 | B.必要非充分条件 | C.充要条件 | D.非充分非必要条件 |
B
解析试题分析:因为向量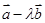 与
与 共线,所以
共线,所以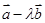
 ,解得
,解得 ,“向量
,“向量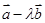 与
与 共线”是“
共线”是“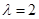 ”的必要非充分条件。
”的必要非充分条件。
考点:向量共线的条件;充分、必要、充要条件的判断。
点评:熟记向量平行和垂直的条件,设 :
:
非零向量垂直的充要条件: ;
;
向量共线的充要条件: 。
。

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
已知命题
 ,命题
,命题
 .则命题
.则命题 是命题
是命题 的
的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知
 则
则 是
是 的 条件
的 条件
| A.充分不必要 | B.必要不充分 |
| C.充要 | D.既不充分又不必要 |
“ ”是“直线
”是“直线 和直线
和直线 垂直”的
垂直”的
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
命题“对 ”的否定是( )
”的否定是( )
| A.不存在x∈R,x3-x2+1≤0 | B. |
C. | D. |
“双曲线的方程为 ”是“双曲线的渐近线方程为
”是“双曲线的渐近线方程为 ”的( )
”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
命题“所有奇数的立方都是奇数”的否定是( )
| A.所有奇数的立方都不是奇数 | B.不存在一个奇数,它的立方是偶数 |
| C.存在一个奇数,它的立方是偶数 | D.不存在一个奇数,它的立方是奇数 |
命题:“ x∈R,
x∈R, ”的否定是( )
”的否定是( )
A. x∈R, x∈R, | B. x∈R, x∈R, |
C. x∈R, x∈R, | D. x∈R, x∈R, |
命题 若
若 ,则
,则 是
是 的充分而不必要条件;命题
的充分而不必要条件;命题 函数
函数 的定义域是
的定义域是 ,则( )
,则( )
A.“ 或 或 ”为假 ”为假 | B.“ 且 且 ”为真 ”为真 |
C. 真 真 假 假 | D. 假 假 真 真 |