题目内容
如图,已知正方体ABCD—A1B
(1)证明四边形BND
(2)求四边形BND
(1)证明:在BB1上取一点P,使B1P=C1N.连结A1P、PN.
∵B1P![]() C1N,∴四边形B1PNC1是平行四边形.
C1N,∴四边形B1PNC1是平行四边形.
∴PN![]() B
B![]()
∴D1N![]() A1P.∵A
A1P.∵A![]() BP,
BP,
∴四边形A1MBP是平行四边形.
∴BM![]() A1P.BM
A1P.BM![]() D1N.
D1N.
∴四边形BND
(2)解析:连结MN,设MN∩BD1=O.
由(1)可知![]() =2
=2![]() ,
,
在△BMD1中,BD1=![]() .
.
又∵当点M运动到AA1中点M0时,易证M0O是异面直线AA1与BD1的公垂线段,且可求得M0O=![]() a,从而点M到BD1的最小距离就是异面直线AA1与BD1之间的距离
a,从而点M到BD1的最小距离就是异面直线AA1与BD1之间的距离![]() a.
a.
∴![]() 的最小值是
的最小值是![]() ×
×![]() a×
a×![]() =
=![]() .
.
∴四边形BMD1N面积的最小值为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 8、如图,已知正方体ABCD-A1B1C1D1的棱长为3,点E,F在线段AB上,点M在线段B1C1上,点N在线段C1D1上,且EF=1,D1N=x,AE=y,M是B1C1的中点,则四面体MNEF的体积( )
8、如图,已知正方体ABCD-A1B1C1D1的棱长为3,点E,F在线段AB上,点M在线段B1C1上,点N在线段C1D1上,且EF=1,D1N=x,AE=y,M是B1C1的中点,则四面体MNEF的体积( )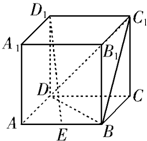 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E为棱AB的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E为棱AB的中点. 如图,已知正方体ABCD-A1B1C1D1的棱长为2,E、F分别是D1C、AB的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,E、F分别是D1C、AB的中点. 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P,Q,R分别是棱AB,CC1,D1A1的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P,Q,R分别是棱AB,CC1,D1A1的中点. (2012•宝山区一模)如图,已知正方体ABCD-A1B1C1D1 的棱长为2,E,F分别是BB1,CD的中点.
(2012•宝山区一模)如图,已知正方体ABCD-A1B1C1D1 的棱长为2,E,F分别是BB1,CD的中点.