题目内容
已知函数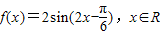 ,
,(1)求出函数f(x)的最小正周期和f(0)的值;
(2)求函数f(x)的单调增区间.
(3)求函数f(x)在区间[0,
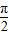 ]上的最小值和最大值,并求出取得最值时x的值.
]上的最小值和最大值,并求出取得最值时x的值.
【答案】分析:(1)根据函数的解析式可求得函数的最小正周期,以及f(0)=2sin(-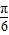 ) 的值.
) 的值.
(2)令 2kπ-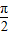 ≤2x-
≤2x-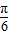 ≤2kπ+
≤2kπ+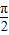 ,k∈z,求得x的范围,可得函数的增区间.
,k∈z,求得x的范围,可得函数的增区间.
(3)由x∈[0,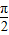 ],利用正弦函数的定义域和值域求得函数f(x)的最值以及取得最值时x的值.
],利用正弦函数的定义域和值域求得函数f(x)的最值以及取得最值时x的值.
解答:解:(1)根据函数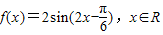 ,可得函数的最小正周期为
,可得函数的最小正周期为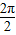 =π,
=π,
f(0)=2sin(-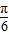 )=2×(-
)=2×(- )=-1.
)=-1.
(2)令 2kπ-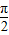 ≤2x-
≤2x-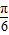 ≤2kπ+
≤2kπ+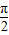 ,k∈z,求得 kπ-
,k∈z,求得 kπ-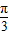 ≤x≤kπ+
≤x≤kπ+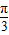 ,
,
故函数的增区间为[kπ-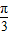 ,kπ+
,kπ+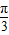 ],k∈z.
],k∈z.
(3)由x∈[0,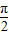 ],可得-
],可得-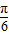 ≤2x-
≤2x-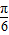 ≤
≤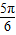 ,
,
故当2x-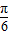 =-
=-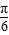 时,即x=0时,sin(2x-
时,即x=0时,sin(2x-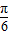 )取得最小值为-
)取得最小值为- ,函数f(x)取得最小值为-1;
,函数f(x)取得最小值为-1;
当2x-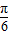 =
=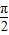 时,即x=
时,即x=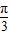 时,sin(2x-
时,sin(2x-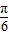 )取得最大值为1,函数f(x)取得最大值为2.
)取得最大值为1,函数f(x)取得最大值为2.
点评:本题主要考查复合三角函数的周期性、单调性的应用,正弦函数的定义域和值域,属于中档题.
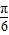 ) 的值.
) 的值.(2)令 2kπ-
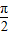 ≤2x-
≤2x-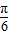 ≤2kπ+
≤2kπ+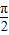 ,k∈z,求得x的范围,可得函数的增区间.
,k∈z,求得x的范围,可得函数的增区间.(3)由x∈[0,
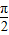 ],利用正弦函数的定义域和值域求得函数f(x)的最值以及取得最值时x的值.
],利用正弦函数的定义域和值域求得函数f(x)的最值以及取得最值时x的值.解答:解:(1)根据函数
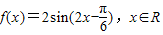 ,可得函数的最小正周期为
,可得函数的最小正周期为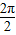 =π,
=π,f(0)=2sin(-
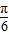 )=2×(-
)=2×(- )=-1.
)=-1.(2)令 2kπ-
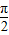 ≤2x-
≤2x-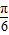 ≤2kπ+
≤2kπ+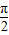 ,k∈z,求得 kπ-
,k∈z,求得 kπ-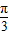 ≤x≤kπ+
≤x≤kπ+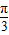 ,
,故函数的增区间为[kπ-
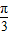 ,kπ+
,kπ+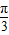 ],k∈z.
],k∈z.(3)由x∈[0,
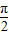 ],可得-
],可得-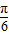 ≤2x-
≤2x-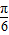 ≤
≤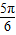 ,
,故当2x-
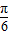 =-
=-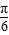 时,即x=0时,sin(2x-
时,即x=0时,sin(2x-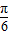 )取得最小值为-
)取得最小值为- ,函数f(x)取得最小值为-1;
,函数f(x)取得最小值为-1;当2x-
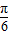 =
=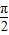 时,即x=
时,即x=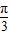 时,sin(2x-
时,sin(2x-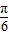 )取得最大值为1,函数f(x)取得最大值为2.
)取得最大值为1,函数f(x)取得最大值为2.点评:本题主要考查复合三角函数的周期性、单调性的应用,正弦函数的定义域和值域,属于中档题.

练习册系列答案
相关题目
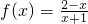 ;
;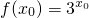 成立,若存在求出x0;若不存在,请说明理由.
成立,若存在求出x0;若不存在,请说明理由.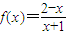 ;
; 成立,若存在求出x;若不存在,请说明理由.
成立,若存在求出x;若不存在,请说明理由. .
. 时,证明函数y=f(x)图象在点
时,证明函数y=f(x)图象在点 处切线的下方;
处切线的下方; ,且a+b+c=1,证明:
,且a+b+c=1,证明: ”;
”; 的最大值.(只指出正确结论,不要求证明)
的最大值.(只指出正确结论,不要求证明)