题目内容
已知椭圆C的中心在原点,焦点在x轴上,它的一个顶点恰好是抛物线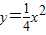 的焦点,离心率等于
的焦点,离心率等于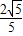 .
.(1)求椭圆C的方程;
(2)过椭圆C的右焦点F作直线l交椭圆C于A、B两点,交y轴于M点,若
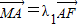 ,
,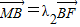 ,求证:λ1+λ2为定值.
,求证:λ1+λ2为定值.
【答案】分析:(1)根据椭圆C的一个顶点恰好是抛物线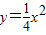 的焦点,离心率等于
的焦点,离心率等于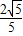 .易求出a,b的值,得到椭圆C的方程.
.易求出a,b的值,得到椭圆C的方程.
(2)设A、B、M点的坐标分别为A(x1,y1),B(x2,y2),设直线l的斜率为k,则直线l的方程是y=k(x-2),然后采用“联立方程”+“设而不求”+“韦达定理”,结合已知中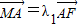 ,
,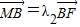 ,求出λ1+λ2值,即可得到结论.
,求出λ1+λ2值,即可得到结论.
解答:解:(1)设椭圆C的方程为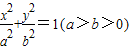 ,则由题意知b=1.…(2分)∴
,则由题意知b=1.…(2分)∴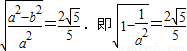 .∴a2=5.…(4分)
.∴a2=5.…(4分)
∴椭圆C的方程为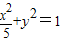 .…(5分)
.…(5分)
(2)设A、B、M点的坐标分别为A(x1,y1),B(x2,y2),M(0,y).
又易知F点的坐标为(2,0).…(6分)
显然直线l存在的斜率,设直线l的斜率为k,则直线l的方程是y=k(x-2).…(7分)
将直线l的方程代入到椭圆C的方程中,消去y并整理得(1+5k2)x2-20k2x+20k2-5=0.…(8分)∴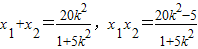 .…(9分)
.…(9分)
又∵ .(11分)∴
.(11分)∴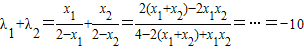 .…(12分)
.…(12分)
点评:本题考查的知识点是椭圆的标准方程,直线与圆锥曲线的综合问题,其中根据已知条件计算出椭圆的标准方程是解答本题的关键.
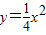 的焦点,离心率等于
的焦点,离心率等于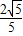 .易求出a,b的值,得到椭圆C的方程.
.易求出a,b的值,得到椭圆C的方程.(2)设A、B、M点的坐标分别为A(x1,y1),B(x2,y2),设直线l的斜率为k,则直线l的方程是y=k(x-2),然后采用“联立方程”+“设而不求”+“韦达定理”,结合已知中
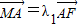 ,
,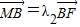 ,求出λ1+λ2值,即可得到结论.
,求出λ1+λ2值,即可得到结论.解答:解:(1)设椭圆C的方程为
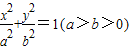 ,则由题意知b=1.…(2分)∴
,则由题意知b=1.…(2分)∴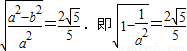 .∴a2=5.…(4分)
.∴a2=5.…(4分)∴椭圆C的方程为
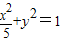 .…(5分)
.…(5分)(2)设A、B、M点的坐标分别为A(x1,y1),B(x2,y2),M(0,y).
又易知F点的坐标为(2,0).…(6分)
显然直线l存在的斜率,设直线l的斜率为k,则直线l的方程是y=k(x-2).…(7分)
将直线l的方程代入到椭圆C的方程中,消去y并整理得(1+5k2)x2-20k2x+20k2-5=0.…(8分)∴
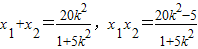 .…(9分)
.…(9分)又∵
 .(11分)∴
.(11分)∴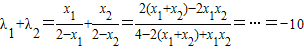 .…(12分)
.…(12分)点评:本题考查的知识点是椭圆的标准方程,直线与圆锥曲线的综合问题,其中根据已知条件计算出椭圆的标准方程是解答本题的关键.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目

 。
。