题目内容
14.计算:sin15°=$\frac{\sqrt{6}-\sqrt{2}}{4}$;$\frac{1+tan15°}{1-tan15°}$=$\sqrt{3}$.分析 由条件利用两角和差的三角公式,求得式子的结果.
解答 解:sin15°=sin(45°-30°)=sin45°cos30°-cos45°sin30°=$\frac{\sqrt{2}}{2}•\frac{\sqrt{3}}{2}$-$\frac{\sqrt{2}}{2}•\frac{1}{2}$=$\frac{\sqrt{6}-\sqrt{2}}{4}$;
$\frac{1+tan15°}{1-tan15°}$=$\frac{tan45°+tan15°}{1-tan45°tan15°}$=tan60°=$\sqrt{3}$,
故答案为:$\frac{{\sqrt{6}-\sqrt{2}}}{4}$;$\sqrt{3}$.
点评 本题主要考查两角和差的三角公式的应用,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.已知A,B分别为椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点,不同两点P,Q在椭圆C上,且关于x轴对称,设直线AP,BQ的斜率分别为m,n,则当$\frac{2b}{a}+\frac{a}{b}+\frac{1}{2mn}$+ln|m|+ln|n|取最小值时,椭圆C的离心率为( )
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{\sqrt{2}}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
2.某次知识竞赛中,四个参赛小队的初始积分都是100分,在答题过程中,各小组每答对1题都可以使自己小队的积分增加5分,若答题过程中四个小队答对的题数分别是4道,7道,7道,2道,则四个小组积分的方差为( )
| A. | 50 | B. | 75.5 | C. | 112.5 | D. | 225 |
9.已知椭圆的标准方程为$\frac{x^2}{10}+{y^2}=1$,则椭圆的焦点坐标为( )
| A. | $({\sqrt{10},0}),({-\sqrt{10},0})$ | B. | $({0,\sqrt{10}}),({0,-\sqrt{10}})$ | C. | (0,3),(0,-3) | D. | (3,0),(-3,0) |
3.已知双曲线C为:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),其左右顶点分别为A、B,曲线上一点P,kPA、kPB分别为直线PA、PB的斜率,且kPA•kPB=3,过左焦点的直线l与双曲线交于两点M,N,|MN|的最小值为4,则双曲线的方程为( )
| A. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1 | B. | $\frac{9{x}^{2}}{4}$-$\frac{3{y}^{2}}{4}$=1 | ||
| C. | $\frac{9{x}^{2}}{4}$-$\frac{3{y}^{2}}{4}$=1和$\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{4}$=1 | D. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1或$\frac{9{x}^{2}}{4}$-$\frac{3{y}^{2}}{4}$=1 |
4.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f($\frac{5π}{6}$)的值为( )


| A. | $-\frac{1}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
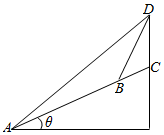 如图所示,在一个坡度一定的山坡AC的顶上有一高度为25m的建筑物CD,为了测量该山坡相对于水平地面的坡角θ,在山坡的A处测得∠DAC=15°,沿山坡前进50m到达B处,又测得∠DBC=45°,根据以上数据可得cosθ=$\sqrt{3}$-1.
如图所示,在一个坡度一定的山坡AC的顶上有一高度为25m的建筑物CD,为了测量该山坡相对于水平地面的坡角θ,在山坡的A处测得∠DAC=15°,沿山坡前进50m到达B处,又测得∠DBC=45°,根据以上数据可得cosθ=$\sqrt{3}$-1.