题目内容
已知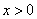 ,函数
,函数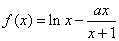
(1)当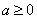 时,讨论函数
时,讨论函数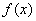 的单调性;
的单调性;
(2)当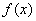 有两个极值点(设为
有两个极值点(设为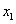 和
和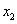 )时,求证:
)时,求证: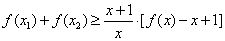 .
.
解:(1)∵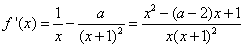 ,
,
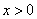 ,考虑分子
,考虑分子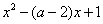
当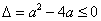 ,即
,即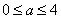 时,在
时,在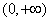 上,
上, 恒成立,此时
恒成立,此时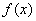 在
在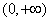 上单调递增;
上单调递增;
当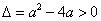 ,即
,即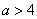 时,方程
时,方程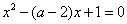 有两个解不相等的实数根:
有两个解不相等的实数根: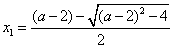 ,
,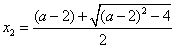 ,显然
,显然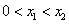 ,
,
∵当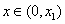 或
或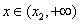 时,
时,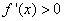 ;当
;当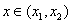 时,
时,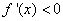 ;
;
∴函数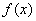 在
在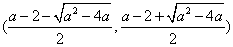 上单调递减,
上单调递减,
在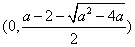 和
和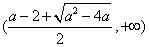 上单调递增.
上单调递增.
(2)∵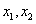 是
是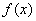 的两个极值点,故满足方程
的两个极值点,故满足方程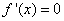 ,
,
即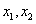 是
是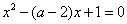 的两个解,∴
的两个解,∴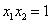 ,
,
∵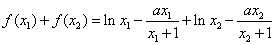

而在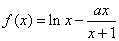 中,
中,
因此,要证明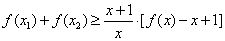 ,
,
等价于证明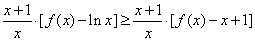
注意到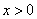 ,只需证明
,只需证明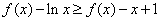
即证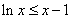
令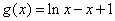 ,则
,则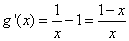 ,
,
当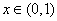 时,
时,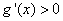 ,函数
,函数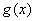 在
在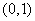 上单调递增;---
上单调递增;---
当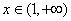 时,
时,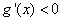 ,函数
,函数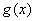 在
在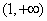 上单调递减;
上单调递减;
因此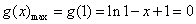 ,从而
,从而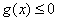 ,即
,即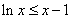 ,原不等式得证.
,原不等式得证.

练习册系列答案
相关题目
 是
是 有实根的( )
有实根的( ) 的单调减区间是 .为 .
的单调减区间是 .为 .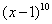 的展开式中
的展开式中 的系数是 .(用数字作答)
的系数是 .(用数字作答)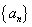 是公比为正数的等比数列,
是公比为正数的等比数列,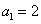 ,
,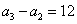 .
.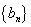 满足:
满足: ,求数列
,求数列 的前n项和
的前n项和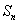 .
. 的正方形
的正方形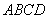 沿对角线
沿对角线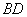 折起,使得平面
折起,使得平面 平面
平面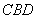 ,形成三棱锥
,形成三棱锥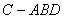 的正视图与俯视图如下图所示,则侧视图的面积为 ( )
的正视图与俯视图如下图所示,则侧视图的面积为 ( )
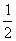 B.
B.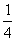 C.
C.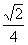 D.
D. 
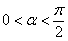 ,
,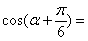
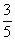 ,则
,则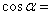 .
.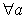 、
、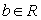 ,运算“
,运算“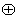 ”、“
”、“ ”定义为:
”定义为: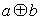 =
=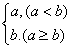 ,
,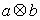 =
=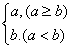 ,则下列各式其中不恒成立的是( )
,则下列各式其中不恒成立的是( )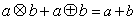 ⑵
⑵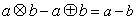
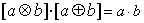 ⑷
⑷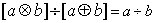
 在点
在点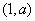 处的切线平行于
处的切线平行于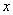 轴,则
轴,则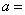 ________.
________.