题目内容
已知函数f（x）=ax2-2x+3在区间（1，2）上是减函数，则a的取值范围是________．
（-∞，
]
分析：由题意可得①a＞0 且 2≤
，或 ②a＜0，且 
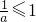，或 ③a=0．分别求出①、②、③的解集，再取并集，即得所求．
解答：由于函数f（x）=ax2-2x+3在区间（1，2）上是减函数，而二次函数的对称轴为x=
，
故有①a＞0 且 2≤，或 ②a＜0，且 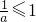，或 ③a=0．
由①可得 0＜a≤，由②可得a＜0，由③得a=0．
综上可得a≤，
故答案为（-∞，]．
点评：本题主要考查二次函数的性质，体现了分类讨论的数学思想，属于基础题．
]分析：由题意可得①a＞0 且 2≤
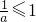，或 ②a＜0，且 ，或 ③a=0．分别求出①、②、③的解集，再取并集，即得所求．解答：由于函数f（x）=ax2-2x+3在区间（1，2）上是减函数，而二次函数的对称轴为x=
，故有①a＞0 且 2≤
，或 ②a＜0，且 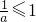，或 ③a=0．由①可得 0＜a≤
，由②可得a＜0，由③得a=0．综上可得a≤
，故答案为（-∞，
]．点评：本题主要考查二次函数的性质，体现了分类讨论的数学思想，属于基础题．
练习册系列答案
相关题目