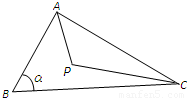
题目内容
点P在△ABC内，并且
+
=6
，设△ABC的面积是△PBC的面积的m倍，那么m=（ ）
| PB |
| PC |
| AP |
| A、1 | ||
B、
| ||
| C、4 | ||
| D、2 |
分析：由点P在三角形ABC内，得M＞1．记
+
=
，交BC与E．再由
+
=6
，得到
，
共线，从而有点E是BC的中点．且E点平分PD．得到
=
，再由△ABC与△PBC同底求出高之比即可．
| PB |
| PC |
| PD |
| PB |
| PC |
| AP |
| AP |
| PD |
| ||
|
| 1 |
| 3 |
解答：解：∵点P在三角形ABC内，
∴M＞1．记
+
=
，交BC与E．
又
+
=6
，
所以
，
共线，
所以点E是BC的中点．且E点平分PD．
所以
=
，
△ABC与△PBC同底，
它们的高之比=
=
m=
故选B
∴M＞1．记
| PB |
| PC |
| PD |
又
| PB |
| PC |
| AP |
所以
| AP |
| PD |
所以点E是BC的中点．且E点平分PD．
所以
| ||
|
| 1 |
| 3 |
△ABC与△PBC同底，
它们的高之比=
| ||
|
| 4 |
| 3 |
m=
| 4 |
| 3 |
故选B
点评：本题主要考查平面向量在平图形中的应用，用向量的加法来刻画平面图形中的点的位置和量的关系．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
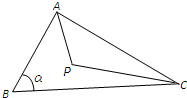如图，点P在△ABC内，AB=CP=2，BC=3，∠P+∠B=π，记∠B=α．
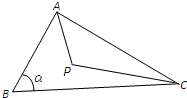如图，点P在△ABC内，AB=CP=2，BC=3，∠P+∠B=π，记∠B=α．
