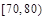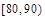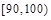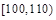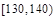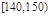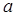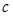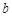题目内容
某同学4次考试的数学（x）、语文（y）成绩在班中的排名如表：| 数学成绩（x） | 6 | 3 | 2 | 1 |
| 语文成绩（y） | 9 | 5 | 4 | 2 |
【答案】分析：利用所给数据，可得回归方程，求出残差平方和，与已知比较，即可得到结论．
解答：解：由于
=3，
=5，那么
=
=
，
∴a=
，此时可得，
，此时的残差平方和
=0.214
已知y=cx2+d来拟合y与x之间的关系为y=0.178x2+2.77，此时的残差平方和1.561
由于0.214＜1.561，可知用
来拟合y与x之间的关系效果最好．
点评：本题考查回归分析的初步应用，考查学生的计算能力，确定回归方程，求出残差平方和是关键．
解答：解：由于
=3，=5，那么==，∴a=
，此时可得，，此时的残差平方和=0.214已知y=cx2+d来拟合y与x之间的关系为y=0.178x2+2.77，此时的残差平方和1.561
由于0.214＜1.561，可知用
来拟合y与x之间的关系效果最好．点评：本题考查回归分析的初步应用，考查学生的计算能力，确定回归方程，求出残差平方和是关键．
练习册系列答案
相关题目
某班一次期中考试之后，从全班同学中随机抽出5位，这5位同学的数学、物理分数见下表：先完成下面（1）～（2）的统计分析，将结果直接写在题中横线上，然后解答第（3）小题．
（1）研究变量y与x的相关关系时，计算得r≈0.94，这说明y与x的相关程度是 ．
（2）求得y与x的线性回归方程之后，该方程所表示的直线一定过点 ．
（3）求y与x的线性回归方程，并估计该班本次考试数学成绩为60分的学生的物理成绩．
| 学生编号 | 1 | 2 | 3 | 4 | 5 |
| 数学分数x | 70 | 75 | 80 | 85 | 90 |
| 物理分数y | 73 | 77 | 80 | 88 | 86 |
（2）求得y与x的线性回归方程之后，该方程所表示的直线一定过点
（3）求y与x的线性回归方程，并估计该班本次考试数学成绩为60分的学生的物理成绩．
（本小题满分12分）
某校共有800名学生，高三一次月考之后，为了了解学生学习情况，用分层抽样方法从中抽出若干学生此次数学成绩，按成绩分组，制成如下的频率分布表：
|
组号 |
第 一 组 |
第 二 组 |
第 三 组 |
第 四 组 |
第 五 组 |
第 六 组 |
第 七 组 |
第 八 组 |
合计 |
|
分组 |
|
|
|
|
|
|
|
|
|
|
频数 |
4 |
6 |
20 |
22 |
18 |
|
10 |
5 |
|
|
频率 |
0.04 |
0.06 |
0.20 |
0.22 |
|
0.15 |
0.10 |
0.05 |
1 |
(Ⅰ) 李明同学本次数学成绩为103分，求他被抽中的概率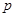
；
(Ⅱ) 为了了解数学成绩在120分以上的学生的心理状态，现决定在第六、七、八组中用分层抽样方法抽取6名学生的成绩，并在这6名学生中在随机抽取2名由心理老师张老师负责面谈，求第七组至少有一名学生与张老师面谈的概率；
(Ⅲ) 估计该校本次考试的数学平均分。
（本小题满分12分）
某校共有800名学生，高三一次月考之后，为了了解学生学习情况，用分层抽样方法从中抽出若干学生此次数学成绩，按成绩分组，制成如下的频率分布表：
|
组号 |
第 一 组 |
第 二 组 |
第 三 组 |
第 四 组 |
第 五 组 |
第 六 组 |
第 七 组 |
第 八 组 |
合计 |
|
分组 |
|
|
|
|
|
|
|
|
|
|
频数 |
4 |
6 |
20 |
22 |
18 |
|
10 |
5 |
|
|
频率 |
0.04 |
0.06 |
0.20 |
0.22 |
|
0.15 |
0.10 |
0.05 |
1 |
（Ⅰ）李明同学本次数学成绩为103分，求他被抽中的概率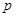
；
（Ⅱ）为了了解数学成绩在120分以上的学生的心理状态，现决定在第六、七、八组中用分层抽样方法抽取6名学生的成绩，并在这6名学生中在随机抽取2名由心理老师张老师负责面谈，求第七组至少有一名学生与张老师面谈的概率；
（Ⅲ）估计该校本次考试的数学平均分。