题目内容
15.已知向量$\vec a,\vec b$满足|$\vec a$|=2,|$\vec b$=3,|2$\vec a$+$\vec b$|=$\sqrt{37}$,则向量$\vec a$与$\vec b$的夹角为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
分析 由已知求出两个向量的数量积,然后利用数量积公式求夹角.
解答 解:因为向量$\vec a,\vec b$满足|$\vec a$|=2,|$\vec b$=3,|2$\vec a$+$\vec b$|=$\sqrt{37}$,
所以|2$\vec a$+$\vec b$|2=37,即4${\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}+4\overrightarrow{a}•\overrightarrow{b}$=37,所以$\overrightarrow{a}•\overrightarrow{b}$=3,
所以向量$\vec a$与$\vec b$的夹角的余弦值为:$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}=\frac{3}{2×3}=\frac{1}{2}$,所以向量$\vec a$与$\vec b$的夹角为$\frac{π}{3}$;
故选:C.
点评 本题考查了向量的平方等于其模的平方以及利用数量积公式求向量的夹角.

练习册系列答案
相关题目
10.设实数x,y满足约束条件$\left\{\begin{array}{l}x-y-2≤0\\ x+2y-5≥0\\ y≤2\end{array}$,则u=$\frac{x+y}{x}$的取值范围是( )
| A. | $[{\frac{4}{3},\frac{3}{2}}]$ | B. | $[{\frac{1}{3},2}]$ | C. | $[{\frac{4}{3},3}]$ | D. | $[{\frac{3}{2},3}]$ |
5.若关于x的方程x2+ax+a2-1=0有一正根和一负根,则实数a的取值范围是( )
| A. | -$\frac{2\sqrt{3}}{3}$<a<-1 | B. | -2<a<2 | C. | -1<a<1 | D. | 1<a<$\frac{2\sqrt{3}}{3}$ |
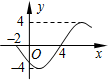 函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<π)的部分图象如图所示,则该函数的解析式为f(x)=4sin($\frac{π}{6}$x-$\frac{2π}{3}$).
函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<π)的部分图象如图所示,则该函数的解析式为f(x)=4sin($\frac{π}{6}$x-$\frac{2π}{3}$).