题目内容
某商场为了促销,当顾客购买的商品的金额达到一定量之后可参加抽奖活动.箱中有4只红球和3只白球,当抽到红球时奖励20元的商品,当抽到白球时,奖励10元的商品(当顾客通过抽奖的方式确定了获奖商品后,即将小球全部放回箱中后).(1)当顾客购买金额超过500元而少于1 000元时,可抽去2个小球,求其中至少有1个红球的概率;
(2)当顾客购买金额超过1 000元时,可抽去3个小球,求他所获奖商品的金额分别是40元和60元的概率.
解:(1)抽取2个小球的基本事件数为21,
至少有1个红球的情况分别为:
A1:抽取2个红球,P(A1)=![]() ;
;
A2:抽取1个红球和1个白球,P(A2)=![]() .
.
所以抽取2个球,至少有1个红球的事件为A1∪A2.
又因为A1、A2为互斥事件,所以P(A1∪A2)=P(A1)+P(A2)=![]() .
.
(2)抽取3个球的基本事件数是35,当抽取的3个球全部为红球时,得60元奖品,概率P(A1)=![]() ;
;
当抽到的3个球中有1个红球和2个白球时,得40元奖品,概率P(A2)=![]() .
.
所以,获奖品40元的概率为![]() ,获60元奖品的概率是
,获60元奖品的概率是![]() .
.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
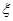 元,求
元,求 元,求
元,求