题目内容
数列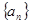 前
前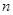 项和
项和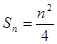 ,数列
,数列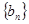 满足
满足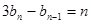 (
(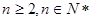 ),
),
(1)求数列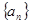 的通项公式;
的通项公式;
(2)求证:当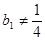 时,数列
时,数列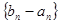 为等比数列;
为等比数列;
(3)在题(2)的条件下,设数列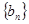 的前
的前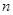 项和为
项和为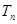 ,若数列
,若数列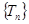 中只有
中只有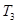 最小,求
最小,求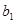 的取值范围.
的取值范围.
【答案】
(1)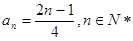 ;(2)详见解析;(3)
;(2)详见解析;(3)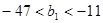 。
。
【解析】
试题分析:(1)本小题主要利用数列公式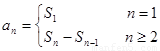 ,可以求得数列
,可以求得数列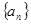 的通项公式
的通项公式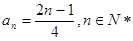 ;
;
(2)本小题通过分析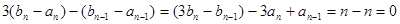 可得
可得 ,根据等比数列的定义可以判定
,根据等比数列的定义可以判定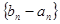 是以
是以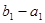 为首项、
为首项、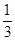 为公比的等比数列;
为公比的等比数列;
(3)本小题首先求得数列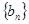 的通项公式
的通项公式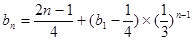 ,然后根据数列
,然后根据数列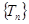 中只有
中只有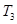 最小可以得出
最小可以得出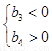 ,即
,即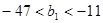 .
.
试题解析:(1)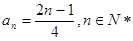 ;
4分
;
4分
(2)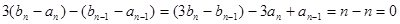 ,
,
所以 ,且
,且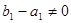 ,
,
所以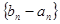 是以
是以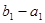 为首项、
为首项、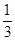 为公比的等比数列; 8分
为公比的等比数列; 8分
(3)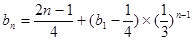 ; 10分
; 10分
因为数列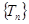 中只有
中只有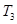 最小,
最小,
所以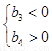 ,解得
,解得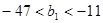 ;
13分
;
13分
此时,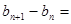
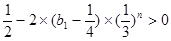 ,
,
于是,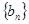 为递增数列,
为递增数列,
所以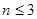 时
时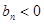 、
、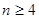 时
时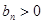 ,符合题意,
,符合题意,
综上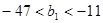 。
15分
。
15分
考点:1.等差数列;2.等比数列;3.数列单调性的判定.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案
相关题目
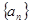 前
前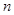 项和
项和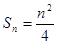 ,数列
,数列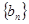 满足
满足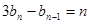 (
(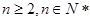 ),
),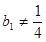 时,数列
时,数列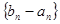 为等比数列;
为等比数列;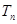 ,若数列
,若数列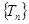 中只有
中只有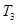 最小,求
最小,求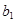 的取值范围.
的取值范围.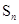 为数列
为数列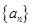 的前
的前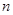 项和,且
项和,且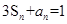 ,数列
,数列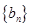 满足
满足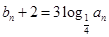 ,数列
,数列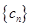 满足
满足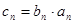 .
.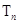 .
.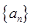 的每项均为正数,首项
的每项均为正数,首项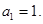 记数列
记数列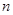 项和为
项和为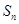 ,满足
,满足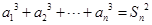 .
.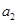 的值及数列
的值及数列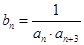 ,记数列
,记数列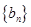 前
前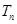 ,求证:
,求证: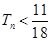 .
.