题目内容
已知函数f(x)=sin( x+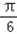 )+sin(x﹣
)+sin(x﹣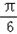 )+cosx+a的最大值为1.
)+cosx+a的最大值为1.
(1)求常数a的值;
(2)求使f (x)≥0成立的x的取值集合;
(3)若 x∈[0,∞],求函数的值域.
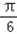 )+sin(x﹣
)+sin(x﹣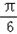 )+cosx+a的最大值为1.
)+cosx+a的最大值为1.(1)求常数a的值;
(2)求使f (x)≥0成立的x的取值集合;
(3)若 x∈[0,∞],求函数的值域.
解:(1)函数f (x)=sin( x+ 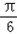 )+sin (x﹣
)+sin (x﹣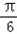 )+cosx+a=
)+cosx+a= 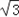 sinx+cosx+a=2sin( x+
sinx+cosx+a=2sin( x+ 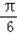 )+a,由最大值为2+a=1,
)+a,由最大值为2+a=1,
解得 a=﹣1.
(2)由f (x)≥0得2sin( x+ 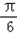 )+a≥0,即 sin( x+
)+a≥0,即 sin( x+ 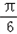 )≥
)≥ ,
,
∴2kπ+ 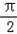 ≥x+
≥x+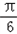 ≥2kπ+
≥2kπ+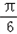 ,
,
故解集为 {x|2kπ≤x≤2kπ+ 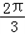 },k∈Z.
},k∈Z.
(3)∵x∈[0,π], ∴ ≤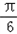 x+
x+ 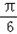 ≤
≤ 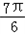 ,
,
∴﹣ ≤sin( x+
≤sin( x+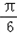 )≤1,
)≤1,
∴﹣2≤2sin( x+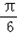 )﹣1≤1,
)﹣1≤1,
故函数f (x)=2sin( x+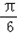 )﹣1 的值域为:[﹣2,1].
)﹣1 的值域为:[﹣2,1].

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
