Question

已知向量=（8cosα，2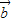），=（sinα-cosα，3），设函数f（α）=•．
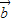（1）求函数f（α）的最大值；
（2）在锐角三角形ABC中，角A、B、C的对边分别问a，b，c，f（A）=6，且△ABC的面积为3，b+c=2+3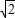，求a的值．

Answer 1

【答案】分析：（1）利用向量的数量积和倍角公式、两角和差的正弦公式及其正弦函数的单调性即可得出；
（2）利用f（A）=6，可得A，再利用三角形的面积公式及已知即可得出b，c，再利用余弦定理即可得出a．
解答：解：（1）=8cosα（sinα-cosα）+6
=8sinαcosα-8cos²α+6
=4sin2α-4（1+cos2α）+2
=+2，
当且仅当时，函数f（α）取得最大值；
（2）由，解得f（A）=6，可得，
∵0，∴，∴，解得A=．
又，解得或．
∴==10，
∴．
点评：熟练掌握向量的数量积和倍角公式、两角和差的正弦公式及其正弦函数的单调性、三角形的面积公式、余弦定理是解题的关键．