题目内容
17.市教科所派4名教研员到3个县调研该县的高三复习备课情况,要求每个县至少派1名教研员,则不同的分配方案种数为( )| A. | 81 | B. | 72 | C. | 64 | D. | 36 |
分析 根据题意,分2步进行分析:①、将4名教研员分成3组,其中一组有2人,②、将分好的三个组,对应要分到的3个县,对3个教研员进行全排列即可,进而由分步计数原理计算可得答案.
解答 解:根据题意,分2步进行分析:
①、将4名教研员分成3组,其中一组有2人,有C42=6种分组方法,
②、将分好的三个组,对应要分到的3个县,有A33=6种对应的方法,
则一共有6×6=36种不同的分配方案;
故选:D.
点评 本题考查分步计数原理的运用,注意题干中“每个县至少派1名教研员”的条件限制.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
2.已知函数$f(x)=\left\{\begin{array}{l}{log_2}x,x≥1\\ f({2x}),0<x<1.\end{array}\right.$则$f[{{{({\frac{1}{2}})}^{\frac{1}{2}}}}]$=( )
| A. | $\frac{3}{2}$ | B. | 1 | C. | $\frac{1}{2}$ | D. | -1 |
9.设变量x,y满足约束条件$\left\{{\begin{array}{l}{x+y-3≥0}\\{x-y-3≤0}\\{y≥1}\end{array}}\right.$,则目标函数z=x+3y的最小值是( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
1.已知方程$\frac{|sinx|}{x}$=k在(0,+∞)上有两个不同的解α,β(α<β),则下面结论正确的是( )
| A. | sinα=-αcosβ | B. | sinα=αcosβ | C. | cosα=βsinβ | D. | sinβ=βsinα |
2.如图所示是一个循环结构的算法,下列说法不正确的是( )
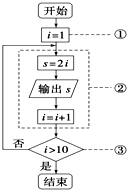

| A. | ①是循环变量初始化,循环就要开始 | |
| B. | ②为循环体 | |
| C. | ③是判断是否继续循环的终止条件 | |
| D. | 输出的S值为2,4,6,8,10,12,14,16,18 |




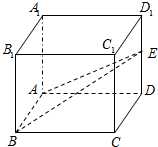 在正方体ABCD-A1B1C1D1中,E是棱DD1的中点,四棱锥E-ABCD的体积为$\frac{4}{3}$,求异面直线BE与B1A1所成的角的大小(结果用反三角函数值表示).
在正方体ABCD-A1B1C1D1中,E是棱DD1的中点,四棱锥E-ABCD的体积为$\frac{4}{3}$,求异面直线BE与B1A1所成的角的大小(结果用反三角函数值表示).