题目内容
已知函数f(x)=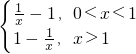 .
.
(Ⅰ)当0<a<b,且f(a)=f(b)时,求 的值;
的值;
(Ⅱ)若存在实数a,b(1<a<b),使得x∈[a,b]时,f(x)的取值范围是[ma,mb](m≠0),求实数m的取值范围.
解:( I)由0<a<b且f(a)=f(b)可得0<a<1<b;
则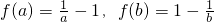
∴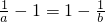 ,即
,即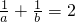 …
…
( II)∵1<a<b,ma<mb,
∴m>0,∴f(x)在[1,+∞)上是增函数,…
∴ ,即
,即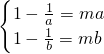 ,∴
,∴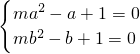 ,
,
∴a,b是方程mx2-x+1=0的两根,…
且关于x的方程mx2-x+1=0由两个大于1的不等实数根,设两个根为x1,x2,则
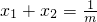 ,
,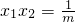 ,
,
∴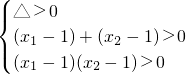 ?
?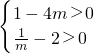 ,…
,…
∴ …
…
分析:(Ⅰ)当0<a<b,利用f(a)=f(b),直接求 的值;
的值;
(Ⅱ)通过1<a<b,使得x∈[a,b]时,f(x)的取值范围是[ma,mb](m≠0),判断函数的单调性,利用函数是值域,列出关系式,得到a,b是方程的两个根,然后求实数m的取值范围.
点评:本题考查函数与方程的思想的应用,函数的值域以及函数的零点,考查分析问题解决问题的能力.
则
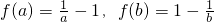
∴
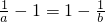 ,即
,即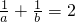 …
…( II)∵1<a<b,ma<mb,
∴m>0,∴f(x)在[1,+∞)上是增函数,…
∴
 ,即
,即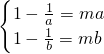 ,∴
,∴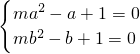 ,
,∴a,b是方程mx2-x+1=0的两根,…
且关于x的方程mx2-x+1=0由两个大于1的不等实数根,设两个根为x1,x2,则
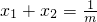 ,
,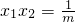 ,
,∴
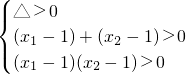 ?
?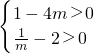 ,…
,…∴
 …
…分析:(Ⅰ)当0<a<b,利用f(a)=f(b),直接求
 的值;
的值;(Ⅱ)通过1<a<b,使得x∈[a,b]时,f(x)的取值范围是[ma,mb](m≠0),判断函数的单调性,利用函数是值域,列出关系式,得到a,b是方程的两个根,然后求实数m的取值范围.
点评:本题考查函数与方程的思想的应用,函数的值域以及函数的零点,考查分析问题解决问题的能力.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|