题目内容
一同学为研究函数f(x)=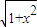 +
+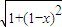 (0≤x≤1)的性质,构造了如图所示的两个边长为1的正方形ABCD和BEFC点P是边BC上的一动点,设CP=x,则AP+PF=f(x),请你参考这些信息,推知函数g(x)=4f(x)-9的零点的个数是 .
(0≤x≤1)的性质,构造了如图所示的两个边长为1的正方形ABCD和BEFC点P是边BC上的一动点,设CP=x,则AP+PF=f(x),请你参考这些信息,推知函数g(x)=4f(x)-9的零点的个数是 .
【答案】分析:由题意可得当A、P、F共线 时,f(x)取得最小值为 <
< ,当P与B或C重合时,f(x)取得最大值为
,当P与B或C重合时,f(x)取得最大值为 +1>
+1> .g(x)=4f(x)-9的零点的个数就是f(x)=
.g(x)=4f(x)-9的零点的个数就是f(x)= 的解的个数,而由题意可得 f(x)=
的解的个数,而由题意可得 f(x)= 的解有2个,从而得出结论.
的解有2个,从而得出结论.
解答:解:由题意可得 函数f(x)= +
+ =AP+PF,当A、P、F共线 时,f(x)取得最小值为
=AP+PF,当A、P、F共线 时,f(x)取得最小值为 <
< ,当P与B或C重合时,f(x)取得最大值为
,当P与B或C重合时,f(x)取得最大值为 +1>
+1> .
.
g(x)=4f(x)-9=0,即 f(x)= .故函数g(x)=4f(x)-9的零点的个数就是f(x)=
.故函数g(x)=4f(x)-9的零点的个数就是f(x)= 的解的个数.
的解的个数.
而由题意可得 f(x)= 的解有2个,
的解有2个,
故答案为 2.
点评:本题主要考查方程的根的存在性及个数判断,体现了化归与转化的数学思想,属于中档题.
 <
< ,当P与B或C重合时,f(x)取得最大值为
,当P与B或C重合时,f(x)取得最大值为 +1>
+1> .g(x)=4f(x)-9的零点的个数就是f(x)=
.g(x)=4f(x)-9的零点的个数就是f(x)= 的解的个数,而由题意可得 f(x)=
的解的个数,而由题意可得 f(x)= 的解有2个,从而得出结论.
的解有2个,从而得出结论.解答:解:由题意可得 函数f(x)=
 +
+ =AP+PF,当A、P、F共线 时,f(x)取得最小值为
=AP+PF,当A、P、F共线 时,f(x)取得最小值为 <
< ,当P与B或C重合时,f(x)取得最大值为
,当P与B或C重合时,f(x)取得最大值为 +1>
+1> .
.g(x)=4f(x)-9=0,即 f(x)=
 .故函数g(x)=4f(x)-9的零点的个数就是f(x)=
.故函数g(x)=4f(x)-9的零点的个数就是f(x)= 的解的个数.
的解的个数.而由题意可得 f(x)=
 的解有2个,
的解有2个,故答案为 2.
点评:本题主要考查方程的根的存在性及个数判断,体现了化归与转化的数学思想,属于中档题.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
 (2013•青岛二模)一同学为研究函数f(x)=
(2013•青岛二模)一同学为研究函数f(x)=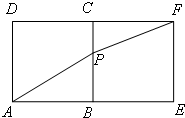
 +
+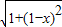 (0≤x≤1)的性质,构造了如图所示的两个边长为1的正方形ABCD和BEFC点P是边BC上的一动点,设CP=x,则AP+PF=f(x),请你参考这些信息,推知函数g(x)=4f(x)-9的零点的个数是 .
(0≤x≤1)的性质,构造了如图所示的两个边长为1的正方形ABCD和BEFC点P是边BC上的一动点,设CP=x,则AP+PF=f(x),请你参考这些信息,推知函数g(x)=4f(x)-9的零点的个数是 .