题目内容
在△ABC中,a,b,c分别为角A,B,C所对的边,向量 =(2a+c,b),
=(2a+c,b), =(cosB,cosC),且
=(cosB,cosC),且 ,
, 垂直.
垂直.
( I)确定角B的大小;
( II)若∠ABC的平分线BD交AC于点D,且BD=1,设BC=x,BA=y,试确定y关于x的函数式,并求边AC长的取值范围.
解:( I)∵ ⊥
⊥ ,∴(2a+c)cosB+bcosC=0,
,∴(2a+c)cosB+bcosC=0,
在△ABC中,由正弦定理得: ,
,
∴a=ksinA,b=ksinB,c=ksinC,代入得
k[(2sinA+sinC)cosB+sinBcosC]=0,∴2sinAcosB+sin(B+C)=0,即sinA(2cosB+1)=0.
∵A,B∈(0,π),∴sinA≠0,
∴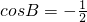 ,解得B=
,解得B= .
.
( II)∵S△ABC=S△ABD+S△BCD, ,
, ,
, ,
,
∴xy=x+y,
∴ .
.
在△ABC中,由余弦定理得:
 =x2+y2+xy=(x+y)2-xy=(x+y)2-(x+y)=
=x2+y2+xy=(x+y)2-xy=(x+y)2-(x+y)= .
.
∵ ,x>0,y>0,∴x+y≥4,
,x>0,y>0,∴x+y≥4,
∴ ,∴
,∴ .
.
∴AC的取值范围是: .
.
分析:(Ⅰ) ⊥
⊥ ?
? ,对此式进行化简得(2a+c)cosB+bcosC=0,再使用正弦定理即可求出角B;
,对此式进行化简得(2a+c)cosB+bcosC=0,再使用正弦定理即可求出角B;
(Ⅱ)先由三角形的面积之间的关系S△ABC=S△ABD+S△BCD得出x+y=xy,再使用余弦定理可得: =
= ,对x+y=xy使用基本不等式,可求出x+y的取值范围,进而可求出AC2的取值范围.
,对x+y=xy使用基本不等式,可求出x+y的取值范围,进而可求出AC2的取值范围.
点评:理解数量积与向量垂直的关系,正确使用正、余弦定理及三角形的面积公式,基本不等式的性质是解决问题的关键.
 ⊥
⊥ ,∴(2a+c)cosB+bcosC=0,
,∴(2a+c)cosB+bcosC=0,在△ABC中,由正弦定理得:
 ,
,∴a=ksinA,b=ksinB,c=ksinC,代入得
k[(2sinA+sinC)cosB+sinBcosC]=0,∴2sinAcosB+sin(B+C)=0,即sinA(2cosB+1)=0.
∵A,B∈(0,π),∴sinA≠0,
∴
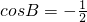 ,解得B=
,解得B= .
.( II)∵S△ABC=S△ABD+S△BCD,
 ,
, ,
, ,
,∴xy=x+y,
∴
 .
.在△ABC中,由余弦定理得:
 =x2+y2+xy=(x+y)2-xy=(x+y)2-(x+y)=
=x2+y2+xy=(x+y)2-xy=(x+y)2-(x+y)= .
.∵
 ,x>0,y>0,∴x+y≥4,
,x>0,y>0,∴x+y≥4,∴
 ,∴
,∴ .
.∴AC的取值范围是:
 .
.分析:(Ⅰ)
 ⊥
⊥ ?
? ,对此式进行化简得(2a+c)cosB+bcosC=0,再使用正弦定理即可求出角B;
,对此式进行化简得(2a+c)cosB+bcosC=0,再使用正弦定理即可求出角B;(Ⅱ)先由三角形的面积之间的关系S△ABC=S△ABD+S△BCD得出x+y=xy,再使用余弦定理可得:
 =
= ,对x+y=xy使用基本不等式,可求出x+y的取值范围,进而可求出AC2的取值范围.
,对x+y=xy使用基本不等式,可求出x+y的取值范围,进而可求出AC2的取值范围.点评:理解数量积与向量垂直的关系,正确使用正、余弦定理及三角形的面积公式,基本不等式的性质是解决问题的关键.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
在△ABC中,∠A、∠B、∠C所对的边长分别是a、b、c.满足2acosC+ccosA=b.则sinA+sinB的最大值是( )
A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|