题目内容
【题目】在平面直角坐标系xOy中,已知向量 ![]() =(
=( ![]() ,﹣
,﹣ ![]() ),
), ![]() =(sinx,cosx),x∈(0,
=(sinx,cosx),x∈(0, ![]() ).
).
(1)若 ![]() ⊥
⊥ ![]() ,求tanx的值;
,求tanx的值;
(2)若 ![]() 与
与 ![]() 的夹角为
的夹角为 ![]() ,求x的值.
,求x的值.
【答案】
(1)解:若 ![]() ⊥
⊥ ![]() ,
,
则 ![]()
![]() =(
=( ![]() ,﹣
,﹣ ![]() )(sinx,cosx)=
)(sinx,cosx)= ![]() sinx﹣
sinx﹣ ![]() cosx=0,
cosx=0,
即 ![]() sinx=
sinx= ![]() cosx
cosx
sinx=cosx,即tanx=1;
(2)解:∵| ![]() |=
|= ![]() ,|
,| ![]() |=
|= ![]() =1,
=1, ![]()
![]() =(
=( ![]() ,﹣
,﹣ ![]() )(sinx,cosx)=
)(sinx,cosx)= ![]() sinx﹣
sinx﹣ ![]() cosx,
cosx,
∴若 ![]() 与
与 ![]() 的夹角为
的夹角为 ![]() ,
,
则 ![]()
![]() =|
=| ![]() ||
|| ![]() |cos
|cos ![]() =
= ![]() ,
,
即 ![]() sinx﹣
sinx﹣ ![]() cosx=
cosx= ![]() ,
,
则sin(x﹣ ![]() )=
)= ![]() ,
,
∵x∈(0, ![]() ).
).
∴x﹣ ![]() ∈(﹣
∈(﹣ ![]() ,
, ![]() ).
).
则x﹣ ![]() =
= ![]()
即x= ![]() +
+ ![]() =
= ![]()
【解析】(1)若 ![]() ⊥
⊥ ![]() ,则
,则 ![]()
![]() =0,结合三角函数的关系式即可求tanx的值;(2)若
=0,结合三角函数的关系式即可求tanx的值;(2)若 ![]() 与
与 ![]() 的夹角为
的夹角为 ![]() ,利用向量的数量积的坐标公式进行求解即可求x的值.
,利用向量的数量积的坐标公式进行求解即可求x的值.
【考点精析】根据题目的已知条件,利用数量积表示两个向量的夹角的相关知识可以得到问题的答案,需要掌握设![]() 、
、![]() 都是非零向量,
都是非零向量,![]() ,
,![]() ,
,![]() 是
是![]() 与
与![]() 的夹角,则
的夹角,则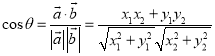 .
.

练习册系列答案
相关题目