题目内容
函数f(x)=cosx(cosx+sinx),x∈[0, ]的值域是
]的值域是
- A.[1,
 ]
] - B.

- C.

- D.

A
分析:利用二倍角公式对函数整理可得,f(x)=cosx(cosx+sinx)= ,结合已知
,结合已知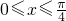 可求答案.
可求答案.
解答:∵f(x)=cosx(cosx+sinx)=cos2x+sinxcosx
= =
= =
=
又∵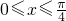 ∴
∴
∴
则1≤f(x)≤
故选A.
点评:本题主要考查了二倍角公式化简三角函数式,y=Asin(ωx+φ)的值域的求解,属于中档试题.
分析:利用二倍角公式对函数整理可得,f(x)=cosx(cosx+sinx)=
 ,结合已知
,结合已知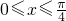 可求答案.
可求答案.解答:∵f(x)=cosx(cosx+sinx)=cos2x+sinxcosx
=
 =
= =
=
又∵
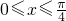 ∴
∴
∴

则1≤f(x)≤

故选A.
点评:本题主要考查了二倍角公式化简三角函数式,y=Asin(ωx+φ)的值域的求解,属于中档试题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目