题目内容
18.已知函数f(x)=$\frac{lnx}{x}$(1)若直线y=kx与曲线f(x)=$\frac{lnx}{x}$相切,求实数k的值;
(2)若e<a<b,比较ab与ba的大小.
分析 (1)设出切点坐标P(a,$\frac{lna}{a}$),求出导函数y′,利用导数的几何意义即k=y′|x=a,再根据切点在切线上,列出关于a和k的方程组,求解即可求得k的值.
(2)由函数f(x)=$\frac{lnx}{x}$,利用函数f(x)的单调性和对数的运算性质即可得到结论.
解答 解:(1)设切点坐标为P(a,$\frac{lna}{a}$),
∵曲线y=$\frac{lnx}{x}$,
∴y′=$\frac{1-lnx}{{x}^{2}}$,
∴k=y′|x=a=$\frac{1-lna}{{a}^{2}}$,①
又∵切点P(a,$\frac{lna}{a}$)在切线y=kx上,
∴$\frac{lna}{a}$=ka,②
由①②,解得a=$\sqrt{e}$,k=$\frac{1}{2e}$,
∴实数k的值为$\frac{1}{2e}$.
(2)由函数f(x)=$\frac{lnx}{x}$,
则f′(x)=$\frac{1-lnx}{{x}^{2}}$,当x>e时,f′(x)<0,
即函数f(x)在x>e时是减函数,
∵e<a<b,
∴$\frac{lna}{a}>\frac{lnb}{b}$,即blna>alnb,即lnab>lnba,
则ab>ba.
点评 本题考查了利用导数研究曲线上某点切线方程.导数的几何意义即在某点处的导数即该点处切线的斜率,解题时要注意运用切点在曲线上和切点在切线上;本题还考查了指数幂的大小比较,根据已知条件,利用函数的单调性是解决本题的关键,综合性较强有一定的难度,属于中档题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
6.圆C1:(x-1)2+(y-1)2=1关于直线x+y=0对称的圆C2的方程为( )
| A. | (x+1)2+(y-1)2=1 | B. | (x-1)2+(y+1)2=1 | ||
| C. | (x+1)2+(y+1)2=1 | D. | (x+1)2+(y-1)2=1或(x-1)2+(y+1)2=1 |
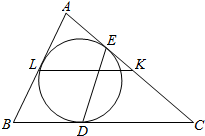 如图,己知L、K分别是△ABC的边AB、AC的中点.△ABC的内切圆⊙l分别与边BC、CA切于点D、E.求证:KL、DE的交点在∠ABC的角平分线上.
如图,己知L、K分别是△ABC的边AB、AC的中点.△ABC的内切圆⊙l分别与边BC、CA切于点D、E.求证:KL、DE的交点在∠ABC的角平分线上.