题目内容
【题目】将直角三角形![]() 沿斜边上的高
沿斜边上的高![]() 折成
折成![]() 的二面角,已知直角边
的二面角,已知直角边![]() ,那么下面说法正确的是( )
,那么下面说法正确的是( )
A. 平面![]() 平面
平面![]() B. 四面体
B. 四面体![]() 的体积是
的体积是![]()
C. 二面角![]() 的正切值是
的正切值是![]() D.
D. ![]() 与平面
与平面![]() 所成角的正弦值是
所成角的正弦值是![]()
【答案】C
【解析】
先由图形的位置关系得到![]() 是二面角
是二面角![]() 的平面角,
的平面角,![]() ,故A不正确;B由于
,故A不正确;B由于![]() 故得到B错误;易知
故得到B错误;易知![]() 为二面角
为二面角![]() 的平面角,
的平面角,![]() ,由题意可知∠BDC为B﹣AD﹣C的平面角,即∠BDC=120°,作DF⊥BC于F,连结AF,sin∠BCO=
,由题意可知∠BDC为B﹣AD﹣C的平面角,即∠BDC=120°,作DF⊥BC于F,连结AF,sin∠BCO=![]() .
.
沿![]() 折后如图,
折后如图,
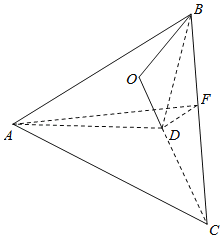
![]() ,易知
,易知![]() 是二面角
是二面角![]() 的平面角,
的平面角,
![]() ,
,![]() 由余弦定理得
由余弦定理得![]()
![]() ,可得
,可得![]() ,过
,过![]() 作
作![]() 于
于![]() ,连接
,连接![]() ,则
,则![]() ,由面积相等得
,由面积相等得![]() ,可得
,可得![]() .
.
根据![]() ,易知
,易知![]() 是二面角
是二面角![]() 的平面角,
的平面角, ![]() 故A 平面
故A 平面![]() 与平面
与平面![]() 不垂直,
不垂直,![]() 错;
错;
B由于![]() ,
,![]() 错;
错;
C易知![]() 为二面角
为二面角![]() 的平面角,
的平面角,![]() ,
,![]() 对;
对;
D故如图,由题意可知∠BDC为B﹣AD﹣C的平面角,即∠BDC=120°,作DF⊥BC于F,连结AF,AF=![]() ,BD=4,DC=8,AD=4,过O作BO垂直BO⊥CO于O,则∠BCO就是BC与平面ACD所成角,BO=2
,BD=4,DC=8,AD=4,过O作BO垂直BO⊥CO于O,则∠BCO就是BC与平面ACD所成角,BO=2![]() ,OD=2,BC=
,OD=2,BC=![]() ,sin∠BCO=
,sin∠BCO=![]() .
.
选![]()

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目


