题目内容
已知函数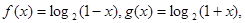 令
令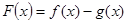
(1)求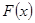 的定义域;
的定义域;
(2)判断函数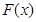 的奇偶性,并予以证明;
的奇偶性,并予以证明;
(3)若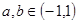 ,猜想
,猜想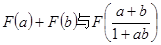 之间的关系并证明.
之间的关系并证明.
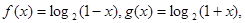 令
令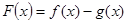
(1)求
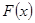 的定义域;
的定义域;(2)判断函数
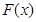 的奇偶性,并予以证明;
的奇偶性,并予以证明;(3)若
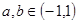 ,猜想
,猜想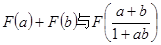 之间的关系并证明.
之间的关系并证明.(1) ;(2)见解析;(3)见解析.
;(2)见解析;(3)见解析.
 ;(2)见解析;(3)见解析.
;(2)见解析;(3)见解析.(1)求定义域是使式子有意义的x的取值集合.
解:(1)由题意可知, ,得定义域为
,得定义域为 -----------4分
-----------4分
(2)定义域关于原点对称,且

所以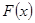 为奇函数----------------------------9分
为奇函数----------------------------9分
(3)当

 ,
,
又

所以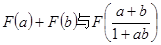 相等-------------------15分
相等-------------------15分
(2)判断奇偶性,一看定义域是否关于原点对称,二看 是否成立.最后下结论.
是否成立.最后下结论.
(3)采用左右共同推证的综合法进行证明.
解:(1)由题意可知,
 ,得定义域为
,得定义域为 -----------4分
-----------4分(2)定义域关于原点对称,且


所以
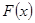 为奇函数----------------------------9分
为奇函数----------------------------9分(3)当


 ,
,又


所以
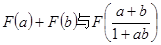 相等-------------------15分
相等-------------------15分(2)判断奇偶性,一看定义域是否关于原点对称,二看
 是否成立.最后下结论.
是否成立.最后下结论.(3)采用左右共同推证的综合法进行证明.

练习册系列答案
相关题目
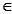 R,函数
R,函数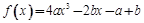 .
.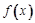 的最大值为|2a-b|﹢a;
的最大值为|2a-b|﹢a;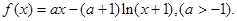
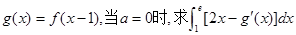 ;
;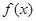 的单调区间;
的单调区间;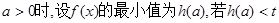 恒成立,求实数t的取值范围。
恒成立,求实数t的取值范围。 ,则
,则 的最小值为( )
的最小值为( )



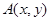 在圆x2+y2=1上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周,已知时间t=0时,点A(
在圆x2+y2=1上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周,已知时间t=0时,点A(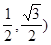 ,则0≤t≤12时,动点A的横坐标x关于t(单位:秒)的函数单调递减区间是( )
,则0≤t≤12时,动点A的横坐标x关于t(单位:秒)的函数单调递减区间是( )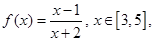 求函数
求函数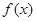 的最大值和最小值.
的最大值和最小值.
 ,猜想
,猜想 的表达式为 ()
的表达式为 () 



 为减函数,
为减函数, 对
对 恒成立,求实数m的取值范围_.
恒成立,求实数m的取值范围_.