题目内容
给出定义：若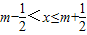
（其中m为整数），则m叫做离实数x最近的整数，记作{x}，即{x}=m在此基础上给出下列关于函数f（x）=|x-{x}|的四个命题：①
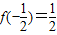；②f（3.4）=-0.4；③
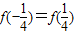；④y=f（x）的定义域为R，值域是
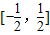；则其中真命题的序号是（ ）
A．①②
B．①③
C．②④
D．③④
【答案】分析：在理解新定义的基础上，求出{-
}、{3.4}、{-
}、{
}对应的整数，进而利用函数f（x）=|x-{x}|可判断①②③的
正误；而对于④易知f（x）=|x-{x}|的值域为[0，
]，则④错误．此时即可作出选择．
解答：解：①∵-1-
＜-
≤-1+
∴{-
}=-1∴f（-
）=|-
-{-
}|=|-
+1|=
∴①正确；
②∵3-
＜3.4≤3+
∴{3.4}=3∴f（3.4）=|3.4-{3.4}|=|3.4-3|=0.4∴②错误；
③∵0-
＜-
≤0+
∴{-
}=0∴f（-
）=|-
-0|=
，
∵0-
＜
≤0+
∴{
}=0∴f（
）=|
-0|=
，∴③正确；
④y=f（x）的定义域为R，值域是[0，
]∴④错误．
故选B．
点评：本题主要考查对于新定义的理解与运用，是对学生能力的考查．
}、{3.4}、{-}、{}对应的整数，进而利用函数f（x）=|x-{x}|可判断①②③的 正误；而对于④易知f（x）=|x-{x}|的值域为[0，
]，则④错误．此时即可作出选择．解答：解：①∵-1-
＜-≤-1+∴{-}=-1∴f（-）=|--{-}|=|-+1|=∴①正确；②∵3-
＜3.4≤3+∴{3.4}=3∴f（3.4）=|3.4-{3.4}|=|3.4-3|=0.4∴②错误；③∵0-
＜-≤0+∴{-}=0∴f（-）=|--0|=，∵0-
＜≤0+∴{}=0∴f（）=|-0|=，∴③正确；④y=f（x）的定义域为R，值域是[0，
]∴④错误．故选B．
点评：本题主要考查对于新定义的理解与运用，是对学生能力的考查．
练习册系列答案
相关题目
（其中m为整数），则m叫做离实数x最近的整数，记作{x}=m．在此基础上给出下列关于函数f（x）=|x-{x}|的四个命题：
；
（k∈Z）对称；
上是增函数．
（其中m为整数），则m叫离实数x最近的整数，记作[x]=m，已知f（x）=|[x]-x|，下列四个命题：
； ②函数f（x）是R上的增函数；
（其中m为整数），则m叫做离实数x最近的整数，记作
，在此基础上给出下列关于函数
的四个命题：①函数
的定义域为
，值域为
；②函数
上是增函数；③函数
；④函数
对称．其中正确命题的序号是 ．
（其中m为整数），则m叫做离实数x最近的整数，记作{x}，即
.在此基础上给出下列关于函数
的四个命题：
的定义域是R，值域是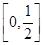
；
对称；
上是增函数．
（其中m为整数），则m叫做离实数x最近的整数，记作{x}，即
，在此基础上给出下列关于函数
的四个命题：
的定义域是R，值域是
；
的图像的对称中心；
上是增函数；