Question

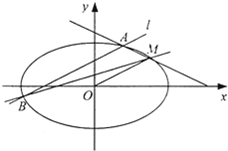已知中心在原点O、焦点在x轴上的椭圆C过点M（2，1），离心率为

3

2

．如图，平行于OM的直线l交椭圆C于不同的两点A，B．
（1）当直线l经过椭圆C的左焦点时，求直线l的方程；
（2）证明：直线MA，MB与x轴总围成等腰三角形．

Answer 1

分析：（1）由e=

c

a

=

3

2

，设椭圆方程为

x2

4b2

+

y2

b2

=1，将M（2，1）代入，得b²=2，由此能求出椭圆C的方程，从而能够求出直线l的方程．
（2）设直线MA，MB的斜率分别为k₁，k₂，A（x₁，y₁），B（x₂，y₂），则k1=

y1-1

x1-2

，k2=

y2-1

x2-2

，设l：y=

1

2

x+m，由

y= 1 2 x+m x2 8 + y2 2 =1

，得x²+2mx+2m²-4=0，推导出k₁+k₂=

y1-1

x1-2

+

y2-1

x2-2

=0，由此能证明直线MA，MB与x轴总围成等腰三角形．

解答：（1）解：∵e=

c

a

=

3

2

，∴设椭圆方程为

x2

4b2

+

y2

b2

=1，
将M（2，1）代入，得

4

4b2

+

1

b2

=1，解得b²=2，
所以椭圆C的方程为

x2

8

+

y2

2

=1，
因此左焦点为（-

6

，0），斜率k1=kOM=

1

2

，
所以直线l的方程为y=

1

2

（x+

6

），即y=

1

2

x+

6

2

．
（2）证明：设直线MA，MB的斜率分别为k₁，k₂，A（x₁，y₁），B（x₂，y₂），
则k1=

y1-1

x1-2

，k2=

y2-1

x2-2

，
∴k₁+k₂=

y1-1

x1-2

+

y2-1

x2-2

=

(y1-1)(x2-2)+(y2-1)(x1-2)

(x1-2)(x2-2)

=

( 1 2 x1+m-1)(x2-2)+( 1 2 x2+m-1)(x1-2)

(x1-2)(x2-2)

=

x1x2+(m-2)(x1+x2)-4(m-1)

(x1-2)(x2-2)

，（*）
设l：y=

1

2

x+m，由

y= 1 2 x+m x2 8 + y2 2 =1

，得x²+2mx+2m²-4=0，
所以x₁+x₂=-2m，x1x2=2m2-4，
代入（*）式，得
k₁+k₂=

2m2-4+(m-2)(-2m)-4(m-1)

(x1-2)(x2-2)

=

2m2-4-2m2+4m-4m+4

(x1-2)(x2-2)

=0．
所以直线MA，MB与x轴总围成等腰三角形．

点评：本题考查直线方程的求法，考查直线MA，MB与x轴总围成等腰三角形的证明．具体涉及到椭圆的简单性质、直线方程的性质、韦达定理等基本知识点．解题时要认真审题，注意合理地进行等价转化．