题目内容
（2013•宿迁一模）已知函数f（x）=lnx-x，h(x)=
．
（1）求h（x）的最大值；
（2）若关于x的不等式xf（x）≥-2x2+ax-12对一切x∈（0，+∞）恒成立，求实数a的取值范围；
（3）若关于x的方程f（x）-x3+2ex2-bx=0恰有一解，其中e是自然对数的底数，求实数b的值．
| lnx | x |
（1）求h（x）的最大值；
（2）若关于x的不等式xf（x）≥-2x2+ax-12对一切x∈（0，+∞）恒成立，求实数a的取值范围；
（3）若关于x的方程f（x）-x3+2ex2-bx=0恰有一解，其中e是自然对数的底数，求实数b的值．
分析：（1）已知h（x）的解析式，对其进行求导，利用导数研究其单调性，从而求解；
（2）因为关于x的不等式xf（x）≥-2x2+ax-12对一切x∈（0，+∞）恒成立，将问题转化为xlnx-x2≥-2x2+ax-12对一切x∈（0，+∞）恒成立，利用常数分离法进行求解；
（3）关于x的方程f（x）-x3+2ex2-bx=0恰有一解，可得
=x2-2ex+b+1恰有一解，构造新函数h（x）=
利用导数研究h（x）的最大值，从而进行求解；
（2）因为关于x的不等式xf（x）≥-2x2+ax-12对一切x∈（0，+∞）恒成立，将问题转化为xlnx-x2≥-2x2+ax-12对一切x∈（0，+∞）恒成立，利用常数分离法进行求解；
（3）关于x的方程f（x）-x3+2ex2-bx=0恰有一解，可得
| lnx |
| x |
| lnx |
| x |
解答：解：（1）因为h(x)=
，(x＞0)，所以h′(x)=
，…（2分）
由h′（x）＞0，且x＞0，得0＜x＜e，由h′（x）＜0，且x＞0，x＞e，…（4分）
所以函数h（x）的单调增区间是（0，e]，单调减区间是[e，+∞），
所以当x=e时，h（x）取得最大值
；…（6分）
（2）因为xf（x）≥-2x2+ax-12对一切x∈（0，+∞）恒成立，
即xlnx-x2≥-2x2+ax-12对一切x∈（0，+∞）恒成立，
亦即a≤lnx+x+
对一切x∈（0，+∞）恒成立，…（8分）
设?(x)=lnx+x+
，因为?′(x)=
=
，
故?（x）在（0，3]上递减，在[3，+∞）上递增，?（x）min=?（3）=7+ln3，
所以a≤7+ln3． …（10分）
（3）因为方程f（x）-x3+2ex2-bx=0恰有一解，
即lnx-x-x3+2ex2-bx=0恰有一解，即
=x2-2ex+b+1恰有一解，
由（1）知，h（x）在x=e时，h(x)max=
，…（12分）
而函数k（x）=x2-2ex+b+1在（0，e]上单调递减，在[e，+∞）上单调递增，
故x=e时，k（x）min=b+1-e2，
故方程
=x2-2ex+b+1恰有一解当且仅当b+1-e2=
，
即b=e2+
-1；
| lnx |
| x |
| 1-lnx |
| x2 |
由h′（x）＞0，且x＞0，得0＜x＜e，由h′（x）＜0，且x＞0，x＞e，…（4分）
所以函数h（x）的单调增区间是（0，e]，单调减区间是[e，+∞），
所以当x=e时，h（x）取得最大值
| 1 |
| e |
（2）因为xf（x）≥-2x2+ax-12对一切x∈（0，+∞）恒成立，
即xlnx-x2≥-2x2+ax-12对一切x∈（0，+∞）恒成立，
亦即a≤lnx+x+
| 12 |
| x |
设?(x)=lnx+x+
| 12 |
| x |
| x2+x-12 |
| x2 |
| (x-3)(x+4) |
| x2 |
故?（x）在（0，3]上递减，在[3，+∞）上递增，?（x）min=?（3）=7+ln3，
所以a≤7+ln3． …（10分）
（3）因为方程f（x）-x3+2ex2-bx=0恰有一解，
即lnx-x-x3+2ex2-bx=0恰有一解，即
| lnx |
| x |
由（1）知，h（x）在x=e时，h(x)max=
| 1 |
| e |
而函数k（x）=x2-2ex+b+1在（0，e]上单调递减，在[e，+∞）上单调递增，
故x=e时，k（x）min=b+1-e2，
故方程
| lnx |
| x |
| 1 |
| e |
即b=e2+
| 1 |
| e |
点评：本题考查利用导数求函数的单调区间的方法，求函数的导数以及对数函数的定义域与单调区间．注意函数的定义域，此题是一道中档题，考查学生计算能力；
练习册系列答案
相关题目
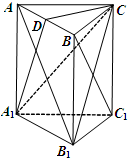（2013•宿迁一模）如图，在直三棱柱ABC-A1B1C1中，AC⊥BC，BC=BB1，D为AB的中点．