题目内容
1.已知函数f(x)=|x-1|+2|x+1|,解不等式f(x)>5.分析 利用绝对值的几何意义,写出分段函数,即可解不等式f(x)>5.
解答 解:f(x)=$\left\{\begin{array}{l}{-3x-1,x≤-1}\\{-x-3,-1<x<1}\\{3x+1,x≥1}\end{array}\right.$,
当x≤-1时,由-3x-1>5得x<-2;
当-1<x≤1时,由-x-3>5得x<-8,无解;
当x>1时,由3x+1>5得x>$\frac{4}{3}$,则x>$\frac{4}{3}$,
综上,所求不等式的解集为:(-∞,-2)∪($\frac{4}{3}$,+∞).
点评 本题主要考查绝对值的意义、绝对值不等式的解法,体现了转化的数学思想,属于基础题.

练习册系列答案
相关题目
9.执行如图所示的程序框图,若输出S的值为$\frac{2014}{2015}$,则判断框内可填入的条件是( )
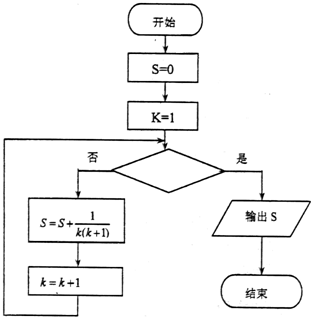

| A. | k>2013 | B. | k>2014 | C. | k>2015 | D. | k>2016 |
6.用反证法证明命题“三角形三个内角至少有一个不大于60°”时,应假设( )
| A. | 三个内角都不大于60° | B. | 三个内角都大于60° | ||
| C. | 三个内角至多有一个大于60° | D. | 三个内角至多有两个大于60° |
13.已知离散型随机变量X的分布列为P(X=1)=$\frac{3}{5}$,P(X=2)=$\frac{3}{10}$,P(X=3)=$\frac{1}{10}$,则X的数学期望E(X)=( )
| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{5}{2}$ | D. | 3 |
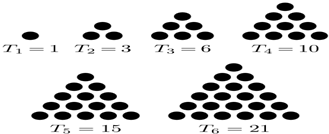 小毕喜欢把数描绘成沙滩上的小石子,他照如图所示摆成了正三角形图案,并把每个图案中总的石子个数叫做“三角形数”,记为Tn,则$\frac{1}{2{T}_{1}}$+$\frac{1}{2{T}_{2}}$+$\frac{1}{2{T}_{3}}$+…+$\frac{1}{2{T}_{2015}}$=$\frac{2015}{2016}$.
小毕喜欢把数描绘成沙滩上的小石子,他照如图所示摆成了正三角形图案,并把每个图案中总的石子个数叫做“三角形数”,记为Tn,则$\frac{1}{2{T}_{1}}$+$\frac{1}{2{T}_{2}}$+$\frac{1}{2{T}_{3}}$+…+$\frac{1}{2{T}_{2015}}$=$\frac{2015}{2016}$.