题目内容

已知F1、F2为椭圆=1(a＞b＞0)的焦点,M为椭圆上一点,MF1垂直于x轴,且∠F1MF2=60°,则椭圆的离心率为(    )

A.                B.

C.              D.

答案：C

解析:∵MF1⊥x轴,∴M点的横坐标为xM=-c.把xM代入椭圆方程=1中,得yM=,如图所示.

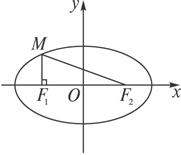
在Rt△MF1F2中,tan∠F1MF2=,即2ac=b2.∴a2-2ac-c2=0.

每一项都除以a2,得-2e-e2=0,

解得e1=或e2=-(舍).

练习册系列答案
相关题目
已知F1，F2为椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的两个焦点，过F2作椭圆的弦AB，若△AF1B的周长为16，椭圆的离心率e=
3
2
，则椭圆的方程为（　　）
A、
x2
4
+
y2
3
=1
B、
x2
16
+
y2
3
=1
C、
x2
16
+
y2
4
=1
D、
x2
16
+
y2
12
=1
已知F1，F2为椭圆E的两个左右焦点，抛物线C以F1为顶点，F2为焦点，设P为椭圆与抛物线的一个交点，如果椭圆离心率e满足|PF1|=e|PF2|，则e的值为
 
．
已知F1、F2为椭圆
x2
25
+
y2
9
=1的两个焦点，点P是椭圆上的一个动点，则|PF1|•|PF2|的最小值是
9
9
．
已知F1、F2为椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)的焦点，B为椭圆短轴的一个端点，
BF1
•
BF2
≥
1
2
F1F2
2则椭圆的离心率的取值范围是
（0，
1
2
]
（0，
1
2
]
．
（2009•荆州模拟）已知F1、F2为椭圆C：
x2
m+1
+
y2
m
=1的两个焦点，P为椭圆上的动点，则△F1PF2面积的最大值为2，则椭圆的离心率e为（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网