Question

已知函数f(x)=

3

sin(2x+φ)-cos(2x+φ)（0＜φ＜π）
（Ⅰ）若φ=

π

3

，用“五点法”在给定的坐标系中，画出函数f（x）在[0，π]上的图象．
（Ⅱ）若f（x）偶函数，求φ
（Ⅲ）在（Ⅱ）的前提下，将函数y=f（x）的图象向右平移

π

6

个单位后，再将得到的图象上各点的横坐标变为原来的4倍，纵坐标不变，得到函数y=g（x）的图象，求g（x）在[0，π]的单调递减区间．

Answer 1

（Ⅰ）当φ=

π

3

时，y=

3

sin(2x+

π

3

)-cos(2x+

π

3

)=

3

2

sin2x+

3

2

cos2x-

1

2

cos2x+

3

2

sin2x
=

3

sin2x+cos2x=2sin(2x+

π

6

)，
列表：

2x+ π 6	π 6	π 2	π	3π 2	2π	13π 6
x	0	π 6	5π 12	2π 3	11π 12	π
y	1	2	0	-2	0	1

故函数y=f（x）在区间[0，π]上的图象是：


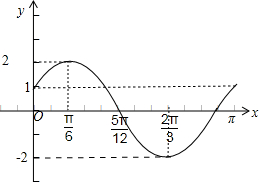
  （6分）
（Ⅱ）f(x)=

3

sin(2x+φ)-cos(2x+φ)=2sin(2x+φ-

π

6

)，…（8分）
因为f（x）为偶函数，则y轴是f（x）图象的对称轴，
所以|sin(φ-

π

6

)|=1，则φ-

π

6

=kπ+

π

2

(k∈Z)，即φ=kπ+

2π

3

(k∈Z)．
又因为0＜φ＜π，故 φ=

2π

3

． …（11分）
（Ⅲ）在（Ⅱ）的前提下，f（x）=2sin（2x+

π

2

）=2cos2x，
故将f（x）的图象向右平移

π

6

个单位，可得函数f（x-

π

6

）的图象，再把所得的图象上各个点的横坐标变为原来的4倍，
可得函数g（x）=f（

x

4

-

π

6

）的图象，故g（x）=f（

x

4

-

π

6

）=2cos（

x

2

-

π

3

）．
令 2kπ≤

x

2

-

π

3

≤2kπ+π，k∈z，解得 4kπ+

2π

3

≤x≤2kπ+

8π

3

，
故g（x）的 单调减区间为[4kπ+

2π

3

，2kπ+

8π

3

]，k∈z．