题目内容
已知{ }是等差数列,其前
}是等差数列,其前 项和为
项和为 ,{
,{ }是等比数列,且
}是等比数列,且 =
= ,
, ,
, .
.
(1)求数列{ }与{
}与{ }的通项公式;
}的通项公式;
(2)记 ,求满足不等式
,求满足不等式 的最小正整数
的最小正整数 的值.
的值.
 }是等差数列,其前
}是等差数列,其前 项和为
项和为 ,{
,{ }是等比数列,且
}是等比数列,且 =
= ,
, ,
, .
.(1)求数列{
 }与{
}与{ }的通项公式;
}的通项公式;(2)记
 ,求满足不等式
,求满足不等式 的最小正整数
的最小正整数 的值.
的值.(1) (2)8
(2)8
 (2)8
(2)8试题分析:(1)设数列
 的公差为
的公差为 ,数列
,数列 的公比为
的公比为 ;
;则

得:
 6分
6分(2)


两式相减得
 ,
, 的最小n值为8. 6分
的最小n值为8. 6分点评:求等差数列等比数列通项时,只需将条件转化为数列的首项和公差公比,进而解方程即可;第二问
 为数列求和,观察其特点采用错位相减法,此法在求和的题目中是常考的方法
为数列求和,观察其特点采用错位相减法,此法在求和的题目中是常考的方法
练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
 角
角 的对边分别为
的对边分别为 ,若
,若 成等差数列,则
成等差数列,则 等于( )
等于( )



 为等差数列,
为等差数列, ,
, ,则
,则 ___________.
___________. 的前5项和
的前5项和 ,则
,则 等于( )
等于( )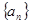 的前
的前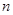 项和为
项和为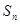 ,若对于任意的正整数
,若对于任意的正整数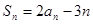 ,
,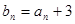 ,求证:数列
,求证:数列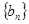 是等比数列,并求出
是等比数列,并求出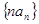 的前
的前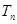 。
。 的前n项和为
的前n项和为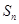 ,且
,且 ,则
,则 =________.
=________.
 ,求n的值;
,求n的值; 的数学公式表示上述结论,并给予证明。
的数学公式表示上述结论,并给予证明。