Question

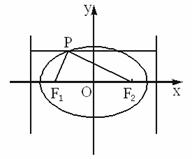
已知椭圆的焦点在x轴上，P为椭圆上一点，F₁、F₂为两焦点，且PF₁⊥PF₂，若P点到两准线的距离分别为6和12，求椭圆的标准方程.

Answer 1

解:如图，设椭圆的方程为=1，焦距为2c，

则|PF₁|=×6，|PF₂|=×12.

∵PF₁⊥PF₂，∴|PF₁|²+|PF₂|²=|F₁F₂|²，

即36·+144·=4c².∴a²=45.

又6+12=×2，∴c=5.

∴b²=a²－c²=20.

∴所求椭圆的方程为=1.

点评:本例的解法是先利用椭圆的第二定义得到|PF₁|=×6，|PF₂|=×12，再由PF₁⊥PF₂写出a、c之间的关系式并结合两准线间的距离等于即得到a²、b²的值.