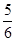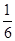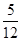题目内容
((本小题满分13分)
已知三个正数 满足
满足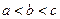 .
.
(Ⅰ)若 是从
是从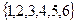 中任取的三个数,求
中任取的三个数,求 能构成三角形三边长的概率;
能构成三角形三边长的概率;
(Ⅱ)若 是从区间
是从区间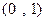 内任取的三个数,求
内任取的三个数,求 能构成三角形三边长的概率.
能构成三角形三边长的概率.
已知三个正数
 满足
满足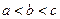 .
.(Ⅰ)若
 是从
是从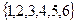 中任取的三个数,求
中任取的三个数,求 能构成三角形三边长的概率;
能构成三角形三边长的概率;(Ⅱ)若
 是从区间
是从区间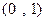 内任取的三个数,求
内任取的三个数,求 能构成三角形三边长的概率.
能构成三角形三边长的概率.解:(Ⅰ)记“ 能构成三角形三边长”为事件A.
能构成三角形三边长”为事件A.
若 能构成三角形,则
能构成三角形,则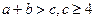 .………
.……… …………1分
…………1分
若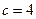 时,则
时,则 ,有1种取法;
,有1种取法;
若 时,则
时,则 ,
, 或
或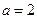 有2种取法;
有2种取法;
若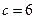 时,有3+1=4种取法
时,有3+1=4种取法
于是共有1+2+4=7种取法.即事件A包含的结果数为7.………………3分
从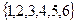 中任取三个数
中任取三个数 且
且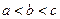 的取法数为
的取法数为 .
.
∴基本事件的所有结果数为20.……………4分
根据古典概型知: 能构成三角形三边长的概率为
能构成三角形三边长的概率为 . ……………6分
. ……………6分
 (Ⅱ)
(Ⅱ) 能构成三角形的三边长当且仅当:
能构成三角形的三边长当且仅当:
 …………………………8分
…………………………8分
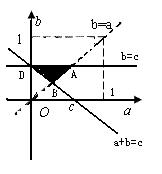
在平面直角坐标系 内对于任意给定的
内对于任意给定的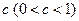 ,作直线
,作直线 ,
,
与直线 及
及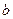 轴正半轴围成三角形ADO.
轴正半轴围成三角形ADO.
再作直线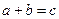 ,则
,则 的面积是
的面积是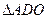 面积的
面积的 (如图).
(如图).
由几何概型的计算方法可知, 能构成三角形三边长的概率为
能构成三角形三边长的概率为 . ……………13分
. ……………13分
 能构成三角形三边长”为事件A.
能构成三角形三边长”为事件A.若
 能构成三角形,则
能构成三角形,则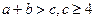 .………
.……… …………1分
…………1分若
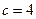 时,则
时,则 ,有1种取法;
,有1种取法;若
 时,则
时,则 ,
, 或
或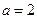 有2种取法;
有2种取法;若
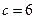 时,有3+1=4种取法
时,有3+1=4种取法于是共有1+2+4=7种取法.即事件A包含的结果数为7.………………3分
从
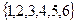 中任取三个数
中任取三个数 且
且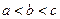 的取法数为
的取法数为 .
.∴基本事件的所有结果数为20.……………4分
根据古典概型知:
 能构成三角形三边长的概率为
能构成三角形三边长的概率为 . ……………6分
. ……………6分 (Ⅱ)
(Ⅱ) 能构成三角形的三边长当且仅当:
能构成三角形的三边长当且仅当: …………………………8分
…………………………8分在平面直角坐标系
 内对于任意给定的
内对于任意给定的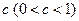 ,作直线
,作直线 ,
,与直线
 及
及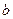 轴正半轴围成三角形ADO.
轴正半轴围成三角形ADO.再作直线
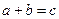 ,则
,则 的面积是
的面积是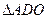 面积的
面积的 (如图).
(如图).由几何概型的计算方法可知,
 能构成三角形三边长的概率为
能构成三角形三边长的概率为 . ……………13分
. ……………13分略

练习册系列答案
相关题目
 ;
; 2分)
2分)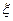 ,求随机变量
,求随机变量 .
. 小题满分12分)
小题满分12分) F三家企业来自河南省,此项工程需要两家企业联合施工,假设每家企业中标的概率相同.
F三家企业来自河南省,此项工程需要两家企业联合施工,假设每家企业中标的概率相同. 少有一家来自山东省的概率是多少?
少有一家来自山东省的概率是多少?



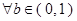 ,则方程
,则方程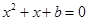 有实根的概率为 ( )
有实根的概率为 ( )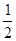
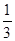
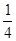

 :“取出的2件产品中至多有1件是二等品”的概率
:“取出的2件产品中至多有1件是二等品”的概率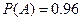 .
.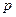 ;
;
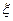 表示取出的2件产品中二等品的件数,求
表示取出的2件产品中二等品的件数,求