Question

已知函数f(x)＝ax²＋bx＋1(a，b为实数)，x∈R，F(x)＝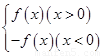

(1)若f(－1)＝0，且函数f(x) ≥0的对任意x属于一切实数成立，求F(x)的表达式；

(2)在 (1)的条件下，当x∈[－2，2]时，g(x)＝f(x)－kx是单调函数，求实数k的取值范围；

 

Answer 1

【答案】

(1) ,  (2) ,

【解析】

试题分析：(1)解析式的求法，可得a与b的关系，再由函数的值域求出各自的值，最后得出解析式。

(2)由(1)已知的解析式，进一步表示出出的解析式，然后得出二次函数的对称轴，利用在闭区间上的单调性得出对称轴的范围，进而求出实数k的取值范围。

试题解析：(1)

又,的值域为,

(2)

对称轴，当或

即或时，是单调函数。

考点：求函数的解析式，恒成立问题，单调性求参量。