题目内容
已知函数f(x)=elnx+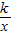 (其中e是自然对数的底数,k为正数)
(其中e是自然对数的底数,k为正数)(I)若f(x)在x处取得极值,且x是f(x)的一个零点,求k的值;
(Ⅱ)若k∈(1,e],求f(x)在区间[
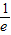 ,1]上的最大值.
,1]上的最大值.
【答案】分析:(Ⅰ)求出原函数的导函数,由f'(x)=0求出x,代入f(x)=0求得k的值;
(Ⅱ)求出原函数的导函数,根据k的范围得到导函数零点的范围,由导函数的零点对给出的区间分段,判出导函数在两区间段内的符号,得到原函数在区间[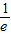 ,1]上端点处取得最大值,通过比较两个端点值的大小得到答案.
,1]上端点处取得最大值,通过比较两个端点值的大小得到答案.
解答:解:(Ⅰ)因为f(x)=elnx+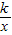 ,所以
,所以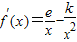 .
.
由已知得f'(x)=0,即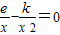 ,∴
,∴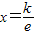
又f(x)=0,即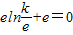 ,∴k=1;
,∴k=1;
(Ⅱ)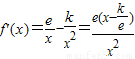 ,
,
∵1<k≤e,∴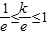 ,
,
由此得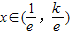 时,f(x)单调递减;
时,f(x)单调递减;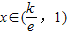 时,f(x)单调递增.
时,f(x)单调递增.
故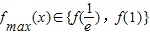
又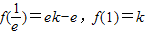 ,当ek-e>k,即
,当ek-e>k,即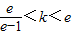 时,
时,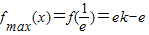 .
.
当ek-e≤k,即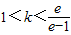 时,fmax(x)=f(1)=k.
时,fmax(x)=f(1)=k.
点评:本题考查了利用导数求闭区间上的最值,考查了分类讨论的数学思想方法,解答的关键是比较端点值的大小,是中高档题.
(Ⅱ)求出原函数的导函数,根据k的范围得到导函数零点的范围,由导函数的零点对给出的区间分段,判出导函数在两区间段内的符号,得到原函数在区间[
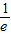 ,1]上端点处取得最大值,通过比较两个端点值的大小得到答案.
,1]上端点处取得最大值,通过比较两个端点值的大小得到答案.解答:解:(Ⅰ)因为f(x)=elnx+
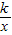 ,所以
,所以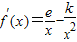 .
.由已知得f'(x)=0,即
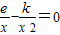 ,∴
,∴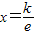
又f(x)=0,即
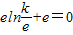 ,∴k=1;
,∴k=1;(Ⅱ)
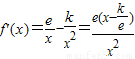 ,
,∵1<k≤e,∴
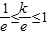 ,
,由此得
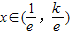 时,f(x)单调递减;
时,f(x)单调递减;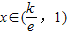 时,f(x)单调递增.
时,f(x)单调递增.故
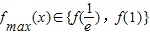
又
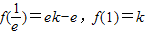 ,当ek-e>k,即
,当ek-e>k,即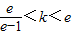 时,
时,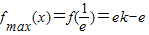 .
.当ek-e≤k,即
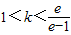 时,fmax(x)=f(1)=k.
时,fmax(x)=f(1)=k.点评:本题考查了利用导数求闭区间上的最值,考查了分类讨论的数学思想方法,解答的关键是比较端点值的大小,是中高档题.

练习册系列答案
相关题目