题目内容
3.实数a,b满足:①2b≥a2-4a;②b≤$\sqrt{4a-{a}^{2}}$;③(|a-2|+|b|-2)(|a-2|+|b|-3)≤0这三个条件,则|a-b-6|的范围是[$\frac{3}{2}$,4+2$\sqrt{2}$].分析 根据题意,把条件转化为线性规划的约束条件,再求目标函数的最值,即可求出对应的取值范围.
解答 解:由题意,4-a2≥0,得0≤a≤4;
设a-2=x,b=y,则①②③式化为
$\left\{\begin{array}{l}{y≥{\frac{1}{2}x}^{2}-2}\\{y≤\sqrt{4{-x}^{2}}}\\{2≤|x|+|y|≤3}\end{array}\right.$,
画出图形,如图所示;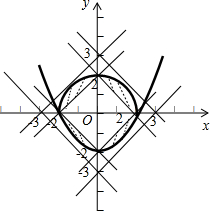
令t=|a-b-6|,则t=|x-y-4|,
所以y=x-4±t;
设y=x+m,利用相切可得2≤m≤2$\sqrt{2}$,-$\frac{5}{2}$≤m≤-2;
$\frac{3}{2}$≤t≤4+2$\sqrt{2}$,
即|a-b-6|的范围是[$\frac{3}{2}$,4+2$\sqrt{2}$].
故答案为:[$\frac{3}{2}$,4+2$\sqrt{2}$].
点评 本题考查了含有绝对值不等式的解法与应用问题,也考查了转化思想与线性规划的应用问题,是难题.

练习册系列答案
相关题目
13.已知x∈(-$\frac{π}{2}$,0),且cosx=$\frac{4}{5}$,则sin2x=( )
| A. | $\frac{24}{25}$ | B. | $\frac{12}{25}$ | C. | -$\frac{24}{25}$ | D. | -$\frac{12}{25}$ |
18.已知函数f(x)=$\frac{3-m•{3}^{x}}{{3}^{x}}$,且函数g(x)=loga(x2+x+2)(a>0,且a≠1)在[-$\frac{1}{4}$,1]上的最大值为2,若对任意x1∈[-1,2],存在x2∈[0,3],使得f(x1)≥g(x2),则实数m的取值范围是( )
| A. | (-∞,-$\frac{2}{3}$] | B. | (-∞,$\frac{1}{3}$] | C. | [$\frac{1}{3}$,+∞) | D. | [-$\frac{1}{3}$,+∞] |
15.λ∈R,下列关系正确的是( )
| A. | |λ$\overrightarrow{a}$|=|λ|$\overrightarrow{a}$ | B. | |λ$\overrightarrow{a}$|=λ|$\overrightarrow{a}$| | C. | 若$\overrightarrow{a}$=$\overrightarrow{0}$,则λ$\overrightarrow{a}$=$\overrightarrow{0}$ | D. | (λ-2)$\overrightarrow{a}$=$λ\overrightarrow{a}$+2$\overrightarrow{a}$ |