题目内容
将正偶数排列如表,其中第i行第j个数表示为aij(i∈N+,j∈N+),例如a32=10,若aij=2012,则i+j= .
【答案】分析:根据题目中给出的图形,归纳总结出各行各列数的个数,分析出各偶数的关系,进而可求出aij=2012时,i,j的值,进而得到答案.
解答:解:由图形可知:
第1行1个偶数,
第2行2个偶数,
…
第n行n个偶数;
∵2012是第1006个偶数,设它在第n行,则之前已经出现了n-1行,共1+2+…+(n-1)=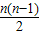 个偶数,
个偶数,
∴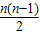 ≤1006,
≤1006,
解得n≤45,
∴2012在第45行,
∵前44行有990个偶数,
∴2012在第45行,第16列,即i=45,j=16,
∴i+j=61,
故答案为61.
点评:本题集数列和图形计数于一体,题目设计新颖,既考查了数列的知识,又考查了归纳推理的过程,是高考考查的重点内容.
解答:解:由图形可知:
第1行1个偶数,
第2行2个偶数,
…
第n行n个偶数;
∵2012是第1006个偶数,设它在第n行,则之前已经出现了n-1行,共1+2+…+(n-1)=
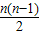 个偶数,
个偶数,∴
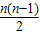 ≤1006,
≤1006,解得n≤45,
∴2012在第45行,
∵前44行有990个偶数,
∴2012在第45行,第16列,即i=45,j=16,
∴i+j=61,
故答案为61.
点评:本题集数列和图形计数于一体,题目设计新颖,既考查了数列的知识,又考查了归纳推理的过程,是高考考查的重点内容.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,将正偶数排列如表,其中第i行第j个数表示为aij(i,j∈N*),例如a43=18,若aij=2010,则i+j=
如图,将正偶数排列如表,其中第i行第j个数表示为aij(i,j∈N*),例如a43=18,若aij=2010,则i+j= 将正偶数排列如表,其中第i行第j个数表示为aij(i∈N+,j∈N+),例如a32=10,若aij=2012,则i+j=
将正偶数排列如表,其中第i行第j个数表示为aij(i∈N+,j∈N+),例如a32=10,若aij=2012,则i+j=
 如图,将正偶数排列如表,其中第i行第j个数表示为aij(i,j∈N*),例如a43=18,若aij=2010,则i+j= .
如图,将正偶数排列如表,其中第i行第j个数表示为aij(i,j∈N*),例如a43=18,若aij=2010,则i+j= . 如图,将正偶数排列如表,其中第i行第j个数表示为aij(i,j∈N*),例如a43=18,若aij=2010,则i+j= .
如图,将正偶数排列如表,其中第i行第j个数表示为aij(i,j∈N*),例如a43=18,若aij=2010,则i+j= .