题目内容
以直角坐标系的原点O为极点,x轴的正半轴为极轴建立极坐标系.已知点P的极坐标为( ,
,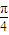 ),直线l过点P,且倾斜角为
),直线l过点P,且倾斜角为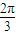 ,方程
,方程 =1所对应的曲线经过伸缩变换
=1所对应的曲线经过伸缩变换 后的图形为曲线C.
后的图形为曲线C.(Ⅰ)求直线l的参数方程和曲线C的直角坐标系方程.
(Ⅱ)直线l与曲线C相交于两点A,B,求|PA|•|PB|的值.
【答案】分析:(Ⅰ)确定P的直角坐标,利用直线l过点P,且倾斜角为 ,可得直线l的参数方程;确定坐标之间的关系,代入方程,化简可得结论;
,可得直线l的参数方程;确定坐标之间的关系,代入方程,化简可得结论;
(Ⅱ)直线l的参数方程,代入曲线方程,利用参数的几何意义,即可求|PA|•|PB|的值.
解答:解:(Ⅰ)P的直角坐标为(1,1)
∵直线l过点P,且倾斜角为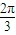 ,∴直线l的参数方程为
,∴直线l的参数方程为 (t为参数)
(t为参数)
∵伸缩变换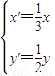 ,∴
,∴
代入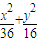 =1,可得
=1,可得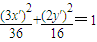 ,即x′2+y′2=4
,即x′2+y′2=4
∴曲线C的直角坐标系方程为x2+y2=4;
(Ⅱ)直线l的参数方程为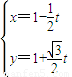 ,代入曲线C可得t2+(
,代入曲线C可得t2+( )t-2=0
)t-2=0
设方程的根为t1,t2,则t1+t2=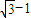 ;t1t2=-2
;t1t2=-2
∴|PA|•|PB|=|t1||t2|=2
点评:本题考查直线的参数方程,考查代入法求轨迹方程,考查直线与椭圆的位置关系,考查参数的几何意义,属于中档题.
 ,可得直线l的参数方程;确定坐标之间的关系,代入方程,化简可得结论;
,可得直线l的参数方程;确定坐标之间的关系,代入方程,化简可得结论;(Ⅱ)直线l的参数方程,代入曲线方程,利用参数的几何意义,即可求|PA|•|PB|的值.
解答:解:(Ⅰ)P的直角坐标为(1,1)
∵直线l过点P,且倾斜角为
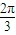 ,∴直线l的参数方程为
,∴直线l的参数方程为 (t为参数)
(t为参数)∵伸缩变换
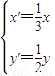 ,∴
,∴
代入
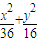 =1,可得
=1,可得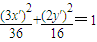 ,即x′2+y′2=4
,即x′2+y′2=4∴曲线C的直角坐标系方程为x2+y2=4;
(Ⅱ)直线l的参数方程为
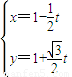 ,代入曲线C可得t2+(
,代入曲线C可得t2+( )t-2=0
)t-2=0设方程的根为t1,t2,则t1+t2=
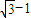 ;t1t2=-2
;t1t2=-2∴|PA|•|PB|=|t1||t2|=2
点评:本题考查直线的参数方程,考查代入法求轨迹方程,考查直线与椭圆的位置关系,考查参数的几何意义,属于中档题.

练习册系列答案
相关题目