题目内容
圆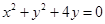 与直线
与直线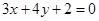 相交于A、B两点,则线段AB的垂直平分线的方程是( )
相交于A、B两点,则线段AB的垂直平分线的方程是( )
A.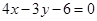 | B.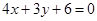 |
C.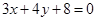 | D.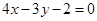 |
A
解析试题分析:根据题意,圆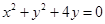 与直线
与直线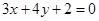 相交于A、B两点,那么可知联立方程组
相交于A、B两点,那么可知联立方程组 ,结合韦达定理的中点纵坐标,然后结合
,结合韦达定理的中点纵坐标,然后结合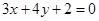 的斜率为
的斜率为 ,可知所求的直线的斜率为
,可知所求的直线的斜率为 ,排除B,C,然后将中点坐标代入可知选A.
,排除B,C,然后将中点坐标代入可知选A.
考点:直线方程的求解
点评:解决的关键是利用弦中点与圆心的连线与线段AB的垂直平分线垂直可知得到斜率,再结合中点坐标公式,属于基础题。

练习册系列答案
相关题目
已知直线l: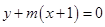 与直线
与直线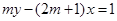 平行,则直线l在
平行,则直线l在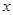 轴上的截距是( )
轴上的截距是( )
| A.1 | B.-1 | C.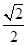 | D.-2 |
设点 ,
, ,直线
,直线 过点
过点 且与线段
且与线段 相交,则
相交,则 的斜率
的斜率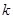 的取值范围是( )
的取值范围是( )
A. 或 或 | B. | C. | D. 或 或 |
直线 的倾斜角是( )
的倾斜角是( )
A. | B. | C.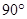 | D.不存在 |
在平面直角坐标系内,一束光线从点A(-3,5)出发,被x轴反射后到达点B(2,7),则这束光线从A到B所经过的距离为( )。
| A.12 | B.13 | C.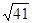 | D.2 + +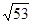 |
三角形的三个顶点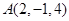 、
、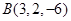 、
、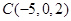 ,则
,则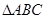 的中线
的中线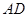 的长为( ).
的长为( ).
| A.49 | B.9 | C.7 | D.3 |
直线 ,当
,当 变动时,所有直线都通过定点
变动时,所有直线都通过定点
| A.(0,0) | B.(0,1) | C.(3,1) | D.(2,1) |
已知过点P(—2,m),Q(m,4)的直线的倾斜角为45°,则m的值为( )
| A.1 | B.2 | C.3 | D.4 |
已知点A(0, –1),点B在直线x–y+1=0上,直线AB垂直于直线x+2y–3=0,则点B的坐标是( )
| A.(–2, –3) | B.(2, 3) | C.(2, 1) | D.(–2, 1) |