题目内容
5件产品中,有3件正品,从中任取2件,
(1)计算恰有1件次品的概率;
(2)计算至少有1件次品的概率.
解:(1)所有的抽法共有 =10种,恰有1件次品的抽法有
=10种,恰有1件次品的抽法有  =6种,
=6种,
故恰有1件次品的概率等于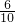 =
= .
.
(2)至少有1件次品的概率等于1减去全是正品的概率,故至少有1件次品的概率等于1- =
= .
.
分析:(1)所有的抽法共有 种,恰有1件次品的抽法有
种,恰有1件次品的抽法有  种,由此求得恰有1件次品的概率.
种,由此求得恰有1件次品的概率.
(2)至少有1件次品的概率等于1减去全是正品的概率,而全是正品的概率等于 ,由此求得结果.
,由此求得结果.
点评:本题主要考查等可能事件的概率,古典概型和对立事件,所求的事件的概率等于用1减去它的对立事件概率,属于
中档题.
 =10种,恰有1件次品的抽法有
=10种,恰有1件次品的抽法有  =6种,
=6种,故恰有1件次品的概率等于
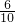 =
= .
.(2)至少有1件次品的概率等于1减去全是正品的概率,故至少有1件次品的概率等于1-
 =
= .
.分析:(1)所有的抽法共有
 种,恰有1件次品的抽法有
种,恰有1件次品的抽法有  种,由此求得恰有1件次品的概率.
种,由此求得恰有1件次品的概率.(2)至少有1件次品的概率等于1减去全是正品的概率,而全是正品的概率等于
 ,由此求得结果.
,由此求得结果.点评:本题主要考查等可能事件的概率,古典概型和对立事件,所求的事件的概率等于用1减去它的对立事件概率,属于
中档题.

练习册系列答案
相关题目

 的绝对值越接近1,若
的绝对值越接近1,若 或
或 时,则
时,则 与
与 的关系完全对应(即有函数关系),在散点图上各个散点均在一条直线上;
的关系完全对应(即有函数关系),在散点图上各个散点均在一条直线上; ,当
,当 平均增加12个单位;
平均增加12个单位; 服从正态分布
服从正态分布
 ,若
,若 ,则
,则 。
。 ,当x每增加一个单位时,
,当x每增加一个单位时, 平均增加12个单位;
平均增加12个单位;