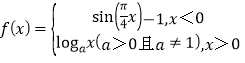题目内容
【题目】已知函数![]() 的图象关于直线
的图象关于直线![]() 对称,且图象上相邻两个最高点的距离为
对称,且图象上相邻两个最高点的距离为![]() .
.
(1)求![]() 和
和![]() 的值;
的值;
(2)当![]() 时,求函数
时,求函数![]() 的最大值和最小值;
的最大值和最小值;
(3)设![]() ,若
,若![]() 的任意一条对称轴与x轴的交点的横坐标不属于区间
的任意一条对称轴与x轴的交点的横坐标不属于区间![]() ,求c的取值范围.
,求c的取值范围.
【答案】(1)![]() ,
,![]() (2)
(2)![]() ;
;![]() .(3)
.(3)![]()
【解析】
(1)由相邻最高点距离得周期,从而可得![]() ,由对称性可求得
,由对称性可求得![]() ;
;
(2)结合正弦函数性质可得最值.
(3)![]() ,先由半个周期大于
,先由半个周期大于![]() 得出
得出![]() 的一个范围,在此范围内再寻找,求出对称轴
的一个范围,在此范围内再寻找,求出对称轴![]() ,由对称轴
,由对称轴![]() 且
且![]() 得
得![]() 的范围.
的范围.
(1)因为![]() 的图象上相邻两个最高点的距离为
的图象上相邻两个最高点的距离为![]() ,
,
所以![]() 的最小正周期
的最小正周期![]() ,而
,而![]() ,
,
又因为![]() 的图象关于直线
的图象关于直线![]() 对称,
对称,
所以![]()
![]() ,即
,即![]()
![]() ,
,
又![]() ,所以
,所以![]() .
.
综上,![]() ,
,![]() .
.
(2)由(1)知![]() ,
,
当![]() 时,
时,![]() ,
,
所以,当![]() 即
即![]() 时,
时,![]() ;
;
当![]() ,即
,即![]() 时,
时,![]() .
.
(3)![]() ,
,
![]() 的任意一条对称轴与x轴的交点的横坐标都不属于区间
的任意一条对称轴与x轴的交点的横坐标都不属于区间![]() ,
,
![]() ,即
,即![]() ,
,
令![]() ,得
,得![]() ,
,
![]() 且
且![]() ,
,
得![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
故所求范围![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】体育测试成绩分为四个等级:优、良、中、不及格.某班50名学生参加测试结果如下:
等级 | 优(86~100分) | 良(75~85分) | 中(60~74分) | 不及格(1~59分) |
人数 | 5 | 21 | 22 | 2 |
(1)估计该班学生体育测试的平均成绩;
(2)从该班任意抽取1名学生,求这名学生的测试成绩为“优”或“良”的概率.