题目内容
1、证明两角差的余弦公式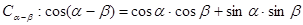 ;
;
2、由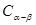 推导两角和的余弦公式
推导两角和的余弦公式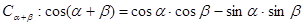 .
.
3、已知△ABC的面积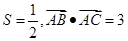 ,且
,且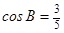 ,求
,求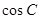 .
.
(1)在平面直角坐标系中,以原点为圆心,作一单位圆,再以原点为顶点,x轴非负半轴为始边分别作角α,β.
设它们的终边分别交单位圆于点P1(cosα,sinα),P2(cosβ,sinβ),即有两单位向量,它们的所成角是|α-β|,根据向量数量积的性质能够证明cos(α-β)=cosαcosβ+sinαsinβ.
(2)先由诱导公式得sin(α+β)=cos(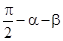 ),再进一步整理为cos[(
),再进一步整理为cos[(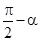 )-β],然后利用和差公式和诱导公式能够得到sin(α+β)=sinαcosβ+cosαsinβ
)-β],然后利用和差公式和诱导公式能够得到sin(α+β)=sinαcosβ+cosαsinβ
2、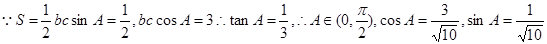
由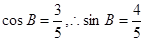 ,
,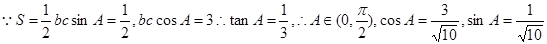
由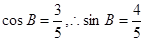 ,所以
,所以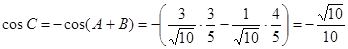
解析

练习册系列答案
相关题目
在△ABC中,若 =
= =
= ,则△ABC是( ).
,则△ABC是( ).
| A.直角三角形 | B.等边三角形 | C.钝角三角形 | D.等腰直角三角形 |
已知 的三个内角满足:
的三个内角满足: ,则
,则 的形状为
的形状为
| A.正三角形 | B.直角三角形 |
| C.等腰直角三角形 | D.等腰三角形或直角三角形 |
 的值
的值
 为锐角,且
为锐角,且
 .
.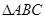 中,角
中,角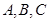 所对边分别为
所对边分别为 ,已知
,已知 .
. 的值;
的值; ,求
,求 的值.
的值. sinA-cos
sinA-cos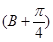 的最大值,并求取得最大值时角A,B的大小.
的最大值,并求取得最大值时角A,B的大小. ,
,
 .
. 的值;
的值; ,
, ,
, ,求
,求 的值
的值 ,
, ,且
,且 ,
, (
( 为常数),求:
为常数),求: 及
及 ;
; 的最小值是
的最小值是 ,求实数
,求实数