题目内容
已知集合
，
，则 ( )
A．  | B． | C． | D．  |
C
解析试题分析：因为
，所以。
考点：集合间的关系；分式不等式的解法。
点评：解分式不等式的步骤是：移项---通分---分式化整式。属于基础题型。
练习册系列答案
相关题目
已知集合
，集合
，则
=
A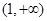． | B． | C． | D． |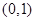
设A={x，y}，集合B={x+1，5}，若A∩B={2}，则A∪B=（ ）
| A．{1，2} | B．{1，5} | C．{2，5} | D．{1，2，5} |
设集合
，
，
,则
=( )
A． | B． | C． | D． |
若集合
，则
（ ）
A． | B． | C． | D． |
已知集合
，
，则
等于
A． | B． | C． | D． |
若集合P＝{1,2,3,4}，Q＝{x|0＜x＜5，x ∈R}，则( )
| A．“x∈P”是“x∈Q”的充分条件但不是必要条件 |
| B．“x∈P”是“x∈Q”的必要条件但不是充分条件 |
| C．“x∈P”是“x∈Q”的充要条件 |
| D．“x∈P”既不是“x∈Q”的充分条件也不是“x∈Q”的必要条件 |
设函数
的定义域与值域都是Ｒ，且单调递增，
，则 （ ）
A． | B． | C．Ａ＝Ｂ | D．A⊆B |
设集合
（ ）
A． | B． | C． | D． |