题目内容
已知函数 .
.
(Ⅰ)若函数f(x)是定义域上的单调函数,求实数a的最小值;
(Ⅱ)方程 .有两个不同的实数解,求实数a的取值范围;
.有两个不同的实数解,求实数a的取值范围;
(Ⅲ)在函数f(x)的图象上是否存在不同两点A(x1,y1),B(x2,y2),线段AB的中点的横坐标为x0,有f′(x0)= 成立?若存在,请求出x0的值;若不存在,请说明理由.
成立?若存在,请求出x0的值;若不存在,请说明理由.
解:(Ⅰ) .(2分)
.(2分)
若函数f(x)在(0,+∞)上递增,
则f′(x)≥0对x>0恒成立,即 对x>0恒成立,
对x>0恒成立,
而当x>0时, .
.
∴a≥1.
若函数f(x)在(0,+∞)上递减,
则f′(x)≤0对x>0恒成立,即 对x>0恒成立,
对x>0恒成立,
这是不可能的.
综上,a≥1.
a的最小值为1.(6分)
(Ⅱ)由 =0,
=0,
得: ,
,
即:a= ,令r(x)=
,令r(x)= ,r′(x)=
,r′(x)= =
=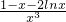
得1-x-2lnx=0的根为1,
所以当0<x<1时,r′(x)>0,则r(x)单调递增,
当x>1时,r′(x)<0,则r(x)单调递减,
所以r(x)在x=1处取到最大值r(1)=1,
又x→0时r(x)→0,又x→+∞时,r(x)→0,
所以要使y= 与y=a有两个不同的交点,则有 0<a<1 …8分
与y=a有两个不同的交点,则有 0<a<1 …8分
(III)假设存在,不妨设0<x1<x2. =
= .(9分)
.(9分)
 .
.
若k=f′(x0),则 ,即
,即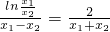 ,即
,即 .(*)(12分)
.(*)(12分)
令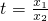 ,
, (0<t<1),
(0<t<1),
则 >0.∴u(t)在0<t<1上是增函数,
>0.∴u(t)在0<t<1上是增函数,
∴u(t)<u(1)=0,
∴(*)式不成立,与假设矛盾.∴k≠f′(x0).
因此,满足条件的x0不存在.(16分)
分析:(I)求出导函数,令导函数大于等于0恒成立或小于等于0恒成立,分离出a,利用基本不等式求出a的范围,从而求出a的最小值.
(Ⅱ)由 =0,得a=
=0,得a= ,令r(x)=
,令r(x)= ,利用导数研究其单调性及最值,从而得出要使y=
,利用导数研究其单调性及最值,从而得出要使y= 与y=a有两个不同的交点,求出实数a的取值范围;
与y=a有两个不同的交点,求出实数a的取值范围;
(III)利用两点连线的斜率公式求出k并且化简k,求出f′(x0)列出方程,通过换元构造新函数,通过导数判断出函数的单调性,求出最值,得到矛盾.
点评:本小题主要考查利用导数研究函数的单调性、利用导数求闭区间上函数的最值、存在性问题等基础知识,考查运算求解能力,考查化归与转化思想.解决是否存在这种探索性的问题,常假设存在去求,若求出则存在,若求不出则不存在.
 .(2分)
.(2分)若函数f(x)在(0,+∞)上递增,
则f′(x)≥0对x>0恒成立,即
 对x>0恒成立,
对x>0恒成立,而当x>0时,
 .
.∴a≥1.
若函数f(x)在(0,+∞)上递减,
则f′(x)≤0对x>0恒成立,即
 对x>0恒成立,
对x>0恒成立,这是不可能的.
综上,a≥1.
a的最小值为1.(6分)
(Ⅱ)由
 =0,
=0,得:
 ,
,即:a=
 ,令r(x)=
,令r(x)= ,r′(x)=
,r′(x)= =
=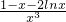
得1-x-2lnx=0的根为1,
所以当0<x<1时,r′(x)>0,则r(x)单调递增,
当x>1时,r′(x)<0,则r(x)单调递减,
所以r(x)在x=1处取到最大值r(1)=1,
又x→0时r(x)→0,又x→+∞时,r(x)→0,
所以要使y=
 与y=a有两个不同的交点,则有 0<a<1 …8分
与y=a有两个不同的交点,则有 0<a<1 …8分(III)假设存在,不妨设0<x1<x2.
 =
= .(9分)
.(9分) .
.若k=f′(x0),则
 ,即
,即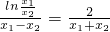 ,即
,即 .(*)(12分)
.(*)(12分)令
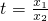 ,
, (0<t<1),
(0<t<1),则
 >0.∴u(t)在0<t<1上是增函数,
>0.∴u(t)在0<t<1上是增函数,∴u(t)<u(1)=0,
∴(*)式不成立,与假设矛盾.∴k≠f′(x0).
因此,满足条件的x0不存在.(16分)
分析:(I)求出导函数,令导函数大于等于0恒成立或小于等于0恒成立,分离出a,利用基本不等式求出a的范围,从而求出a的最小值.
(Ⅱ)由
 =0,得a=
=0,得a= ,令r(x)=
,令r(x)= ,利用导数研究其单调性及最值,从而得出要使y=
,利用导数研究其单调性及最值,从而得出要使y= 与y=a有两个不同的交点,求出实数a的取值范围;
与y=a有两个不同的交点,求出实数a的取值范围;(III)利用两点连线的斜率公式求出k并且化简k,求出f′(x0)列出方程,通过换元构造新函数,通过导数判断出函数的单调性,求出最值,得到矛盾.
点评:本小题主要考查利用导数研究函数的单调性、利用导数求闭区间上函数的最值、存在性问题等基础知识,考查运算求解能力,考查化归与转化思想.解决是否存在这种探索性的问题,常假设存在去求,若求出则存在,若求不出则不存在.

练习册系列答案
相关题目
已知函数 的定义域为
的定义域为 ,若
,若 在
在 上为增函数,则称
上为增函数,则称 为“一阶比增函数”;若
为“一阶比增函数”;若 在
在 上为增函数,则称
上为增函数,则称 为“二阶比增函数”.我们把所有“一阶比增函数”组成的集合记为
为“二阶比增函数”.我们把所有“一阶比增函数”组成的集合记为 ,所有“二阶比增函数”组成的集合记为
,所有“二阶比增函数”组成的集合记为 .
.
(Ⅰ)已知函数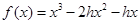 ,若
,若 且
且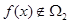 ,求实数
,求实数 的取值范围;
的取值范围;
(Ⅱ)已知 ,
, 且
且 的部分函数值由下表给出,
的部分函数值由下表给出,
|
|
|
|
|
|
|
|
|
|
|
|
求证: ;
;
(Ⅲ)定义集合
请问:是否存在常数 ,使得
,使得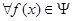 ,
, ,有
,有 成立?若存在,求出
成立?若存在,求出 的最小值;若不存在,说明理由.
的最小值;若不存在,说明理由.
已知函数![]() 的定义域为
的定义域为![]() ,若
,若![]() 在
在![]() 上为增函数,则称
上为增函数,则称![]() 为“一阶比增函数”;若
为“一阶比增函数”;若![]() 在
在![]() 上为增函数,则称
上为增函数,则称![]() 为“二阶比增函数”.
为“二阶比增函数”.
我们把所有“一阶比增函数”组成的集合记为![]() ,所有“二阶比增函数”组成的集合记为
,所有“二阶比增函数”组成的集合记为![]() .
.
(Ⅰ)已知函数![]() ,若
,若![]() 且
且![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)已知![]() ,
,![]() 且
且![]() 的部分函数值由下表给出,
的部分函数值由下表给出,
|
|
|
|
|
|
|
|
|
|
|
|
求证:![]() ;
;
(Ⅲ)定义集合![]()
请问:是否存在常数![]() ,使得
,使得![]() ,
,![]() ,有
,有![]() 成立?若存在,求出
成立?若存在,求出![]() 的最小值;若不存在,说明理由.
的最小值;若不存在,说明理由.
已知函数![]() 的定义域为
的定义域为![]() ,若
,若![]() 在
在![]() 上为增函数,则称
上为增函数,则称![]() 为“一阶比增函数”;若
为“一阶比增函数”;若![]() 在
在![]() 上为增函数,则称
上为增函数,则称![]() 为“二阶比增函数”.
为“二阶比增函数”.
我们把所有“一阶比增函数”组成的集合记为![]() ,所有“二阶比增函数”组成的集合记为
,所有“二阶比增函数”组成的集合记为![]() .
.
(Ⅰ)已知函数![]() ,若
,若![]() 且
且![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)已知![]() ,
,![]() 且
且![]() 的部分函数值由下表给出,
的部分函数值由下表给出,
|
|
|
|
|
|
|
|
|
|
|
求证:![]() ;
;
(Ⅲ)定义集合![]()
请问:是否存在常数![]() ,使得
,使得![]() ,
,![]() ,有
,有![]() 成立?若存在,求出
成立?若存在,求出![]() 的最小值;若不存在,说明理由.
的最小值;若不存在,说明理由.


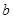
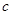




 的定义域为
的定义域为 ,部分函数值如表所示,其导函数的图象如图所示,若正数
,部分函数值如表所示,其导函数的图象如图所示,若正数 ,
, 满足
满足 ,则
,则 的取值范围是( )
的取值范围是( ) 



 B.
B. C.
C. D.
D.